题目内容
21.设函数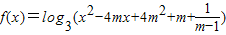 ,其中m是实数,设M={m|m>1}
,其中m是实数,设M={m|m>1}(1)求证:当m∈M时,f(x)对所有实数x都有意义;反之,如果f(x)对所有实数x都有意义,则m∈M;
(2)当m∈M时,求函数f(x)的最小值;
(3)求证:对每一个m∈M,函数f(x)的最小值都不小于1.
【答案】分析:(1)对数的真数构造函数通过m>1,推出对数的真数大于0,所以当m∈M时,f(x)对所有实数x都有意义;通过f(x)对所有实数x都有意义,求出m的范围说明m∈M.
(2)利用基本不等式以及函数的单调性直接求解即可.
(3)通过函数的最小值以及函数的单调性,直接判断对每一个m∈M,函数f(x)的最小值都不小于1.
解答:解:(1)函数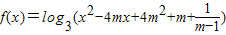 ,
,
令t=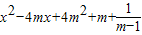
若m>1,则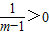 ,∴t>0.
,∴t>0.
若t>0,则△=(4m)2-4(4m2+m+ )=
)=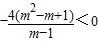 ,
,
∵m2-m+1=(m- )2+
)2+ >0,
>0,
∴m>1,即m∈M.
(2)当m∈M时,t=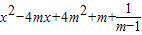
=(x-2m)2+m+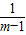 ≥m+
≥m+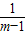 ,(x=2m时取等号).
,(x=2m时取等号).
又函数y=log3t在定义域上是增函数,
∴x=2m时f(x)有最小值log3(m+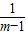 ).
).
(3)∵m+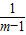 =m-1+
=m-1+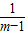 +1,
+1,
又m>1,∴m-1+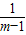 +1≥3,当且仅当m-1=
+1≥3,当且仅当m-1=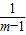 ,即m=2时取等号.
,即m=2时取等号.
又函数y=log3t在定义域上是增函数,
所以log3(m+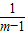 )≥1,
)≥1,
∴对每一个m∈M,函数f(x)的最小值都不小于1.
点评:本题考查函数的单调性,函数的最小值的求法,基本不等式的应用,考查分析问题解决问题的能力,计算能力.
(2)利用基本不等式以及函数的单调性直接求解即可.
(3)通过函数的最小值以及函数的单调性,直接判断对每一个m∈M,函数f(x)的最小值都不小于1.
解答:解:(1)函数
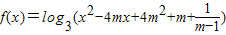 ,
,令t=
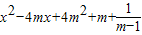
若m>1,则
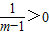 ,∴t>0.
,∴t>0.若t>0,则△=(4m)2-4(4m2+m+
 )=
)=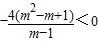 ,
,∵m2-m+1=(m-
 )2+
)2+ >0,
>0,∴m>1,即m∈M.
(2)当m∈M时,t=
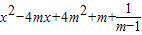
=(x-2m)2+m+
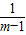 ≥m+
≥m+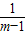 ,(x=2m时取等号).
,(x=2m时取等号).又函数y=log3t在定义域上是增函数,
∴x=2m时f(x)有最小值log3(m+
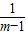 ).
).(3)∵m+
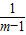 =m-1+
=m-1+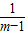 +1,
+1,又m>1,∴m-1+
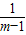 +1≥3,当且仅当m-1=
+1≥3,当且仅当m-1=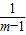 ,即m=2时取等号.
,即m=2时取等号.又函数y=log3t在定义域上是增函数,
所以log3(m+
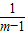 )≥1,
)≥1,∴对每一个m∈M,函数f(x)的最小值都不小于1.
点评:本题考查函数的单调性,函数的最小值的求法,基本不等式的应用,考查分析问题解决问题的能力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
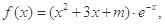 (其中
(其中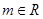 ,
,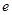 是自然对数的底数)
是自然对数的底数)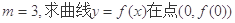 处的切线方程;
处的切线方程; 上有两个极值点.
上有两个极值点.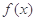 的极小值大于e.
的极小值大于e. ,其中m是实数
,其中m是实数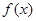 有零点,求m的取值范围;(7分)
有零点,求m的取值范围;(7分)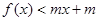 的解集为A,若
的解集为A,若 ,求m的取值范围。(7分)
,求m的取值范围。(7分)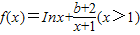 ,其中b为实数.
,其中b为实数.