题目内容
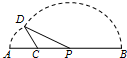 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )分析:在△CPD中,利用CP+CD>PD,CD+PD>CP,可得2<x<4.在△CPD中,设∠DCP=θ,由余弦定理可得cosθ=
=
.利用平方关系可得sinθ=
,利用三角形的面积计算公式可得f(x)=
×CP×CD×sinθ=2
,利用二次函数的单调性即可得出.
| 22+x2-(6-x)2 |
| 2×2×x |
| 3x-8 |
| x |
| 1-cos2θ |
| 1 |
| 2 |
| -2(x-3)2+2 |
解答:解:∵CP=x,CP+PB=8-2=6,
∴CP=6-x=PD.
在△CPD中,∵CP+CD>PD,CD+PD>CP
,∴x+2>6-x,2+6-x>x,
解得2<x<4.
在△CPD中,设∠DCP=θ,由余弦定理可得cosθ=
=
.
∴sinθ=
=
,
∴f(x)=
×CP×CD×sinθ=
×x×2×sinθ=xsinθ=x
=2
∴当且仅当x=3时,f(x)取得最大值,f(3)=2
.
故选A.
∴CP=6-x=PD.
在△CPD中,∵CP+CD>PD,CD+PD>CP
,∴x+2>6-x,2+6-x>x,
解得2<x<4.
在△CPD中,设∠DCP=θ,由余弦定理可得cosθ=
| 22+x2-(6-x)2 |
| 2×2×x |
| 3x-8 |
| x |
∴sinθ=
| 1-cos2θ |
1-(
|
∴f(x)=
| 1 |
| 2 |
| 1 |
| 2 |
1-(
|
| -2(x-3)2+2 |
∴当且仅当x=3时,f(x)取得最大值,f(3)=2
| 2 |
故选A.
点评:本题考查了三角形三边的大小关系、余弦定理、平方关系、三角形的面积计算公式、二次函数的单调性等基础知识与基本技能方法,属于难题.

练习册系列答案
相关题目
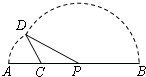 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为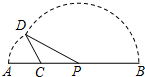 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段BC上的一动 点,点A绕点C旋转后与点B绕点P旋转后重合于点D,设CP=x,△PCD的面积为f(x),则f(x)的最大值为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段BC上的一动 点,点A绕点C旋转后与点B绕点P旋转后重合于点D,设CP=x,△PCD的面积为f(x),则f(x)的最大值为 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).