题目内容
 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段BC上的一动 点,点A绕点C旋转后与点B绕点P旋转后重合于点D,设CP=x,△PCD的面积为f(x),则f(x)的最大值为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段BC上的一动 点,点A绕点C旋转后与点B绕点P旋转后重合于点D,设CP=x,△PCD的面积为f(x),则f(x)的最大值为2
| 2 |
2
.| 2 |
分析:本题要根据实际情况计算出定义域与函数的零点,可以看出所给的条件是△CPD,故可根据其是三角形求出自变量的范围.面积表达式可以用海伦公式求出,对所得的函数求导,令导数为0,根据函数的单调性可求出函数的最大值.
解答:解:三角形的周长是一个定值8,故其面积可用海伦公式表示出来即f(x)=
=
,
∴f′(x)=
由题意,DC=2,CP=x,DP=6-x
∵△CPD为f(x),∴
解得x∈(2,4)
令 f′(x)=0,解得x=3
∵x∈(2,3)f'(x)>0,x∈(3,4)f'(x)<0
∴f(x)的最大值为f(3)=2
故答案为2
.
| 4×(4-x)×(4-6+x)×2 |
| -8x2+48x-64 |
∴f′(x)=
| -16x+48 | ||
|
由题意,DC=2,CP=x,DP=6-x
∵△CPD为f(x),∴
|
令 f′(x)=0,解得x=3
∵x∈(2,3)f'(x)>0,x∈(3,4)f'(x)<0
∴f(x)的最大值为f(3)=2
| 2 |
故答案为2
| 2 |
点评:本题考查根据实际问题选择函数类型,本题中求函数解析式用到了海伦公式,学习中积累一些知识储备,视野开阔,易找出简单的解题方法.本题考查到了复合函数求导公式,有一定的综合性.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
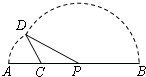 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为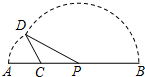 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的定义域为 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕着C旋转后与点B绕点P旋转后重合于点D,设CP=x,△CPD的面积为f(x).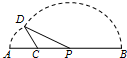 如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )
如图,线段AB=8,点C在线段AB上,且AC=2,P为线段CB上一动点,点A绕点C旋转后与点B绕点P旋转后重合于点D.设CP=x,△CPD的面积为f(x).则f(x)的最大值为( )