题目内容
若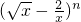 的展开式中第三项是常数项,则n=________,展开式中各项的系数和为________.
的展开式中第三项是常数项,则n=________,展开式中各项的系数和为________.
6 1
分析:根据二项式定理,易得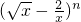 的通项,由题意,第三项是常数项,则有r=2时,T3为常数项,可得
的通项,由题意,第三项是常数项,则有r=2时,T3为常数项,可得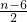 =0,解可得n的值,进而可得二项式为(
=0,解可得n的值,进而可得二项式为( -
- )6,令x=1可得展开式中各项的系数和.
)6,令x=1可得展开式中各项的系数和.
解答:根据题意,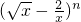 的通项为Tr+1=Cnr(
的通项为Tr+1=Cnr( )n-r•(-
)n-r•(- )r=(-1)r•Cnr(2)r•(
)r=(-1)r•Cnr(2)r•(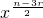 )
)
由题意,第三项是常数项,则有r=2时,T3=(-1)2•Cn2(2)2•(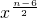 )=4Cn2•(
)=4Cn2•(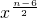 ),为常数项,
),为常数项,
即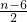 =0,解可得n=6;
=0,解可得n=6;
则该二项式为( -
- )6,令x=1可得,可得(1-
)6,令x=1可得,可得(1- )6=1,
)6=1,
则其展开式中各项的系数和为1.
故答案为:6;1.
点评:本题考查二项式定理的应用与二项式系数的性质,解此类题目要注意区分展开式中各项的系数和与二项式系数和.
分析:根据二项式定理,易得
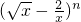 的通项,由题意,第三项是常数项,则有r=2时,T3为常数项,可得
的通项,由题意,第三项是常数项,则有r=2时,T3为常数项,可得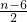 =0,解可得n的值,进而可得二项式为(
=0,解可得n的值,进而可得二项式为( -
- )6,令x=1可得展开式中各项的系数和.
)6,令x=1可得展开式中各项的系数和.解答:根据题意,
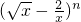 的通项为Tr+1=Cnr(
的通项为Tr+1=Cnr( )n-r•(-
)n-r•(- )r=(-1)r•Cnr(2)r•(
)r=(-1)r•Cnr(2)r•(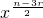 )
)由题意,第三项是常数项,则有r=2时,T3=(-1)2•Cn2(2)2•(
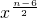 )=4Cn2•(
)=4Cn2•(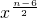 ),为常数项,
),为常数项,即
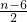 =0,解可得n=6;
=0,解可得n=6;则该二项式为(
 -
- )6,令x=1可得,可得(1-
)6,令x=1可得,可得(1- )6=1,
)6=1,则其展开式中各项的系数和为1.
故答案为:6;1.
点评:本题考查二项式定理的应用与二项式系数的性质,解此类题目要注意区分展开式中各项的系数和与二项式系数和.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
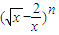 的展开式中第三项是常数项,则n= ,展开式中各项的系数和为 .
的展开式中第三项是常数项,则n= ,展开式中各项的系数和为 .