题目内容
已知函数 则下列关于函数
则下列关于函数 的零点个数的判断正确的是 ( )
的零点个数的判断正确的是 ( )
 则下列关于函数
则下列关于函数 的零点个数的判断正确的是 ( )
的零点个数的判断正确的是 ( )A.当 时,有3个零点;当 时,有3个零点;当 时,有2个零点 时,有2个零点 |
B.当 时,有4个零点;当 时,有4个零点;当 时,有1个零点 时,有1个零点 |
C.无论 为何值,均有2个零点 为何值,均有2个零点 |
D.无论 为何值,均有4个零点 为何值,均有4个零点 |
B
分四种情况讨论.(1)x>1时,lnx>0,∴y=f(f(x))+1=ln(lnx)+1,此时的零点为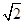
(2)0<x<1时lnx<0,∴y=f(f(x))+1=" k" lnx+1,则k>0时,有一个零点,k<0时,没有零点,
(3)若x<0,k x+1≤0时,y=f(f(x))+1= k 2x+ k +1,则k>0时,有一个零点,k<0时,没有零点,
(4)若x<0,k x+1>0时,y=f(f(x))+1=lnx(k x+1)+1,则k>0时,有一个零点,k<0时,没有零点,
综上可知,当k>0时,有4个零点;当k<0时,有1个零点
故选B
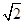
(2)0<x<1时lnx<0,∴y=f(f(x))+1=" k" lnx+1,则k>0时,有一个零点,k<0时,没有零点,
(3)若x<0,k x+1≤0时,y=f(f(x))+1= k 2x+ k +1,则k>0时,有一个零点,k<0时,没有零点,
(4)若x<0,k x+1>0时,y=f(f(x))+1=lnx(k x+1)+1,则k>0时,有一个零点,k<0时,没有零点,
综上可知,当k>0时,有4个零点;当k<0时,有1个零点
故选B

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
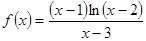 的零点有
的零点有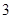 个
个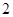 个
个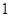 个
个 个
个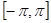 上,
上,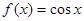 的零点有( )个
的零点有( )个 的图象是连续不断的,有如下
的图象是连续不断的,有如下 对应值表:
对应值表: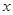






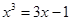 一根
一根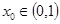 ,则再经过两次计算后,
,则再经过两次计算后, 所在的开区间为 .
所在的开区间为 .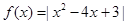 .
.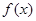 的单调区间,并指出其增减性;
的单调区间,并指出其增减性;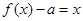 至少有三个不相等的实数根,求实数a的取值范围.
至少有三个不相等的实数根,求实数a的取值范围. ,若
,若 时,
时, 。
。 ,若
,若 ,则
,则 _______.
_______.