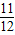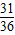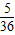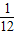题目内容
抛掷两次骰子,两个点的和不等于8的概率为
- A.

- B.

- C.

- D.

B
分析:设抛掷两次骰子,两个点分别为x、y,所有的(x,y)共有6×6=36个,由于满足两个点的和等于8的(x,y)有5个,由此可以求得两个点的和等于8的概率,再用1减去此概率,即得所求.
解答:设抛掷两次骰子,两个点分别为x、y,则 1≤x≤6、1≤y≤6,故所有的(x,y)共有6×6=36个.
其中,满足两个点的和等于8的(x,y)有:(2,6)、(6,2)、(3,5)、(5,3)、(4,4),共有5个,
故抛掷两次骰子,两个点的和等于8的概率为 ,
,
故抛掷两次骰子,两个点的和不等于8的概率为 1- =
= ,
,
故选B.
点评:本题考查古典概型及其概率计算公式的应用,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.
分析:设抛掷两次骰子,两个点分别为x、y,所有的(x,y)共有6×6=36个,由于满足两个点的和等于8的(x,y)有5个,由此可以求得两个点的和等于8的概率,再用1减去此概率,即得所求.
解答:设抛掷两次骰子,两个点分别为x、y,则 1≤x≤6、1≤y≤6,故所有的(x,y)共有6×6=36个.
其中,满足两个点的和等于8的(x,y)有:(2,6)、(6,2)、(3,5)、(5,3)、(4,4),共有5个,
故抛掷两次骰子,两个点的和等于8的概率为
 ,
,故抛掷两次骰子,两个点的和不等于8的概率为 1-
 =
= ,
,故选B.
点评:本题考查古典概型及其概率计算公式的应用,所求的事件的概率与它的对立事件的概率之间的关系,属于基础题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
抛掷两个骰子,至少有一个4点或5点出现时,就说这些试验成功,则在10次试验中,成功次数ξ的期望是( )
A、
| ||
B、
| ||
C、
| ||
D、
|