题目内容
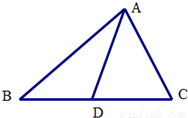
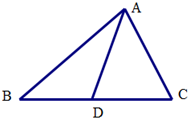
 已知AD是△ABC边BC的中线,用坐标法证明:|AB|2+|AC|2=2(|AD|2+|DC|2)$\end{array}$.
已知AD是△ABC边BC的中线,用坐标法证明:|AB|2+|AC|2=2(|AD|2+|DC|2)$\end{array}$.
【答案】分析:以D为坐标原点、BC所在直线为x轴,建立直角坐标系如图,设C(c,0),B(-c,0),A(a,b),分别计算出|AB|2、
|AC|2、|AD|2和|DC|2关于a、b、c的式子,再进行比较即可证出原等式成立.
解答: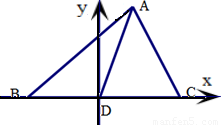 解:以D为坐标原点,BC所在直线为x轴建立如图坐标系
解:以D为坐标原点,BC所在直线为x轴建立如图坐标系
设C(c,0),B(-c,0),A(a,b)
∴|AB|2=(a+c)2+b2,|AC|2=(a-c)2+b2
可得:|AB|2+|AC|2=[(a+c)2+b2]+[(a-c)2+b2]=2(a2+b2+c2)
∵|AD|2=a2+b2,|AC|2=c2.
∴2(|AD|2+|AC|2)=2(a2+b2+c2)
因此,|AB|2+|AC|2=2(|AD|2+|AC|2),原命题得证
点评:本题给出三角形的中线,求证与之相关的一个平方等式成立.着重考查了三角形中线的性质和运用坐标法证明几何性质等知识,属于基础题.
|AC|2、|AD|2和|DC|2关于a、b、c的式子,再进行比较即可证出原等式成立.
解答:
 解:以D为坐标原点,BC所在直线为x轴建立如图坐标系
解:以D为坐标原点,BC所在直线为x轴建立如图坐标系设C(c,0),B(-c,0),A(a,b)
∴|AB|2=(a+c)2+b2,|AC|2=(a-c)2+b2
可得:|AB|2+|AC|2=[(a+c)2+b2]+[(a-c)2+b2]=2(a2+b2+c2)
∵|AD|2=a2+b2,|AC|2=c2.
∴2(|AD|2+|AC|2)=2(a2+b2+c2)
因此,|AB|2+|AC|2=2(|AD|2+|AC|2),原命题得证
点评:本题给出三角形的中线,求证与之相关的一个平方等式成立.着重考查了三角形中线的性质和运用坐标法证明几何性质等知识,属于基础题.

练习册系列答案
相关题目
已知D是△ABC边BC延长线上一点,记
=λ
+(1-λ)
.若关于x的方程2sin2x-(λ+1)sinx+1=0在[0,2π)上恰有两解,则实数λ的取值范围是( )
| AD |
| AB |
| AC |
| A、λ<-2 | ||
| B、λ<-4 | ||
C、λ=-2
| ||
D、λ<-4或λ=-2
|