题目内容
已知直线z的极坐标方程为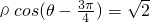 ,点A的极坐标为(4,
,点A的极坐标为(4, ),则点A到直线l的距离为
),则点A到直线l的距离为
- A.

- B.1
- C.

- D.2
C
分析:利用两角差的余弦函数展开方程,把极坐标方程化为普通方程,求出A的直角坐标,利用点到直线的距离公式求解即可.
解答:因为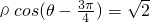 可化为:
可化为: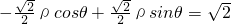 ,
,
直线z的直角坐标方程为:x-y+2=0,
点A的极坐标为(4, ),它的直角坐标(2
),它的直角坐标(2 ,2
,2 ),
),
则A到直线的距离为:d=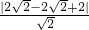 =
= .
.
故选C.
点评:本题是基础题,考查极坐标与直角坐标的互化,点到直线的距离公式的应用,考查计算能力.
分析:利用两角差的余弦函数展开方程,把极坐标方程化为普通方程,求出A的直角坐标,利用点到直线的距离公式求解即可.
解答:因为
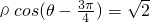 可化为:
可化为: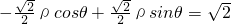 ,
,直线z的直角坐标方程为:x-y+2=0,
点A的极坐标为(4,
 ),它的直角坐标(2
),它的直角坐标(2 ,2
,2 ),
),则A到直线的距离为:d=
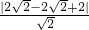 =
= .
.故选C.
点评:本题是基础题,考查极坐标与直角坐标的互化,点到直线的距离公式的应用,考查计算能力.

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
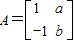 ,A的一个特征值λ=2,其对应的特征向量是
,A的一个特征值λ=2,其对应的特征向量是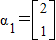 .
.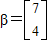 ,计算A2β的值.
,计算A2β的值.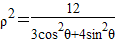 ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为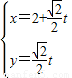 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和.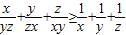 .
. =M
=M ,试求二阶矩阵M.
,试求二阶矩阵M. ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和. .
.