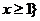题目内容
函数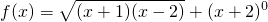 ,则其定义域为
,则其定义域为
- A.{x|x≤-1或x≥2}
- B.{x|-1≤x≤2}
- C.{x|x≤-1或x≥2,且x≠-2}
- D.{x|x<-2或x≥1}
C
分析:求该函数的定义域,需要根式内部的代数式大于等于0,同时保证零指数幂的底数不等于0,求解后取交集.
解答:要使原函数有意义,需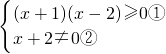 ,
,
解①得:x≤-1或x≥2,
解②得:x≠-2,
所以,函数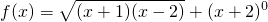 的定义域为{x|x≤-1或x≥2,且x≠-2}.
的定义域为{x|x≤-1或x≥2,且x≠-2}.
故选C.
点评:本题属于以函数的定义域为平台,求集合的交集的基础题,也是高考中常考的题型.
分析:求该函数的定义域,需要根式内部的代数式大于等于0,同时保证零指数幂的底数不等于0,求解后取交集.
解答:要使原函数有意义,需
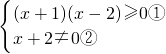 ,
,解①得:x≤-1或x≥2,
解②得:x≠-2,
所以,函数
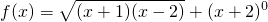 的定义域为{x|x≤-1或x≥2,且x≠-2}.
的定义域为{x|x≤-1或x≥2,且x≠-2}.故选C.
点评:本题属于以函数的定义域为平台,求集合的交集的基础题,也是高考中常考的题型.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
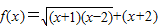 ,则其定义域为( )
,则其定义域为( )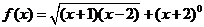 ,则其定义域为
(
)
,则其定义域为
(
)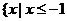 或
或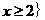 B.
B.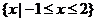
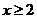 ,且
,且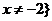 D.
D. 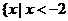 或
或