题目内容

已知
e
是单位向量，且满足|
a
+
e
|=|
a
-2
e
|，则向量
a
在
e
方向上的投影是（　　）
分析：根据向量投影的概念，
a
在
e
方向上的投影为
a
•
e
|
e
|
．将|
a
+
e
|=|
a
-2
e
|两边平方并整理化简得
a
•
e
=
1
2
，问题获解．
解答：解：将|
a
+
e
|=|
a
-2
e
|两边平方，得出
a
2+2
a
•
e
+ 
e
2=
a
2-4
a
•
e
+4
e
2
化简整理得出，
a
•
e
=
1
2

根据向量投影的概念
向量
a
在
e
方向上的投影是
a
•
e
|
e
|
=
1
2

故选C．
点评：向量的投影是有严格定义的概念：向量
a
在
b
方向上的投影的表达式为|
a
|cos＜
a
，
b
＞=
a
•
b
|
b
|
．是计算的根据．
练习册系列答案
相关题目
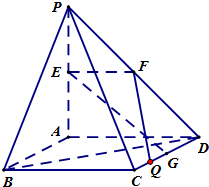精英家教网（理）如图，PA⊥平面ABCD，四边形ABCD是正方形，PA=AD=2，点E、F、G分别为线段PA、PD和CD的中点．
（1）求异面直线EG与BD所成角的大小；
（2）在线段CD上是否存在一点Q，使得点A到平面EFQ的距离恰为
4
5
？若存在，求出线段CQ的长；若不存在，请说明理由．
（文）已知坐标平面内的一组基向量为
e
1=(1，sinx)，
e
2=(0，cosx)，其中x∈[0，
π
2
)，且向量
a
=
1
2
e
1+
3
2
e
2．
（1）当
e
1和
e
2都为单位向量时，求|
a
|；
（2）若向量
a
和向量
b
=(1，2)共线，求向量
e
1和
e
2的夹角．

已知向量与是夹角为60°的两个单位向量，且＝2＋，＝－e＋2，求与的夹角为

[　　]
A．

30°

B．

60°

C．

120°

D．

150°
已知
e
是单位向量，且满足|
a
+
e
|=|
a
-2
e
|，则向量
a
在
e
方向上的投影是（　　）
A．2B．1C．
1
2
D．
1
4

已知e是单位向量，求满足a∥e且a·e =－18的向量a=_______.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网