题目内容
若方程
表示圆，且过点
可作该圆的两条切线，则实数
的取值范围为 ．
解析考点：直线与圆的位置关系．
分析：方程x2+y2-2ax+a2+2a-3=0表示圆，求出圆心（a，0）以及a＜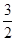 
，A（a，a）在圆外，可求a 的范围．
解：圆x2+y2-2ax+a2+2a-3=0的圆心（a，0）且a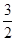＜，而且（a，a）在圆外，即有a2＞3-2a，解得a＜-3或 1＜a＜．
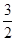故答案为：a＜-3或 1＜a＜．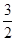
练习册系列答案
相关题目
题目内容
若方程表示圆，且过点可作该圆的两条切线，则实数的取值范围为 ．
解析考点：直线与圆的位置关系．
分析：方程x2+y2-2ax+a2+2a-3=0表示圆，求出圆心（a，0）以及a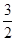＜ ，A（a，a）在圆外，可求a 的范围．
解：圆x2+y2-2ax+a2+2a-3=0的圆心（a，0）且a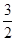＜，而且（a，a）在圆外，即有a2＞3-2a，解得a＜-3或 1＜a＜．
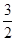故答案为：a＜-3或 1＜a＜．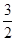
，下列四个命题
表示圆心在第四象限的圆，则实数
的范围为 .
始终平分圆
的周长，则
的取值范围是 。
交于M、N两点，且M、N关于直线
对称，则不等式组
表示的平面区域的面积是 。
的直线l将圆C：(x-2)2+y2=4分成两段弧，当劣弧所对
的圆心角最小时，直线l的斜率k= ▲ 
的直线
与曲线
有公共点，则直线