题目内容
已知双曲线 :
: ,若存在过右焦点
,若存在过右焦点 的直线与双曲线
的直线与双曲线 相交于
相交于 两点且
两点且 ,则双曲线离心率的最小值为( )
,则双曲线离心率的最小值为( )
A. | B. | C. | D. |
C
解析试题分析:因为过右焦点的直线与双曲线 相交于
相交于 两点且
两点且 ,故直线与双曲线相交只能如图所示的情况,即A点在双曲线的左支,B点在右支,设
,故直线与双曲线相交只能如图所示的情况,即A点在双曲线的左支,B点在右支,设 ,右焦点
,右焦点 ,因为
,因为 ,所以
,所以 ,由图可知,
,由图可知, ,所以
,所以 故
故 ,即
,即 ,即
,即 ,选C.
,选C.
考点:平面向量的坐标运算、双曲线性质、双曲线离心率、不等式的性质.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
四棱锥 中,底面
中,底面 是平行四边形,
是平行四边形,
 则直线
则直线 与底面
与底面 的关系是( )
的关系是( )
| A.平行 | B.垂直 |
| C.在平面内 | D.成60°角 |
已知向量 ,
, ,且
,且 ,则
,则 等于( )
等于( )
A. | B. | C. | D. |
已知向量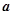
 ,
,
 ,且
,且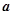 //
// ,则
,则 等于 ( )
等于 ( )
A. | B.2 | C. | D. |
已知点 ,
, 则与
则与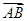 同方向的单位向量是( )
同方向的单位向量是( )
A. | B. | C. | D. |
已知向量
 ,向量
,向量
 ,且
,且 ,则
,则 的值是( )
的值是( )
A. | B. | C.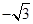 | D. |
已知向量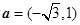 ,
, .若
.若 与
与 共线,则实数
共线,则实数 ( )
( )
A. | B. | C. | D. |
已知向量
 若
若 ,则
,则 的最小值为( )
的最小值为( )
| A.2 | B.4 | C. | D. |
 ,其中
,其中 与
与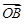 的夹角为
的夹角为 ,
, 的夹角为
的夹角为 ,且
,且 ,若
,若 ,则( )
,则( )



