题目内容
已知函数y=x+
有如下性质：如果常数a＞0,那么该函数在(0，
］上是减函数，在［
,+∞)上是增函数.(1)如果函数y=x+
(x＞0)的值域为［6,+∞)，求b的值；
(2)研究函数y=x2+
(常数c＞0)在定义域内的单调性，并说明理由；
(3)对函数y=x+
和y=x2+
(常数a＞0)作出推广，使它们都是你所推广的函数的特例，研究推广后的函数的单调性(只须写出结论，不必证明)，并求函数f(x)=(x2+
)n+(
+x)n(n是正整数)在区间［
,2］上的最大值和最小值(可利用你的研究结论).
解析：(1)函数y=x+(x＞0)在(0,]上是减函数，在［,+∞)上是增函数，
∴该函数在x=处取得最小值2.
令2=6得b=log29.
(2)方法1：设t=x2≥0,显然函数y=t+在(0,]上是减函数，在［,+∞)上是增函数.
令x2≤，得-
≤x≤
,
令x2≥
,得x≥
或x≤-
.
又∵t=x2在(-∞,0]上是减函数，在［0,+∞)上是增函数，
于是利用复合函数的单调性知，函数y=x2+
,在(-∞,-
]上是减函数，在［-
,0)上是增函数，在(0，
]上是减函数，［
,+∞)上是增函数.
方法2：∵y′=2x-
=2x-
,
令y′=0则x=±
,又∴x≠0,
于是
x | (-∞，- | - | (- | 0 | (0, |
| ( |
f′(x) | - | 0 | + |
| - | 0 | + |
f(x) | ↘ | 极小值 | ↗ |
| ↘ | 极大值 | ↗ |
)
,0)
)
,+∞)∴y=x2+
(c＞0)的单调增区间是［-
,0),［
,+∞);
单调递减区间是(-∞,-
],(0,
].
(3)推广结论：当n是正奇数时，函数y=xn+
(常数a＞0)是奇函数，故在(-∞,-
]上是增函数，在［-
,0)上是减函数，
在(0,
]上是减函数，在［
,+∞)上是增函数.
而当n是正偶数时，函数y=xn+
(常数a＞0)是偶函数，
在(-∞,-
]上是减函数，在［-
,0)上是增函数，
在(0,
]上是减函数，在［
,+∞)上是增函数.
当x=1时，有最小值(1的任意次幂都是1)，
∴F(x)min=F(1)=(1+1)n+(1+1)n=2n+1,
F(x)max=F(
)=F(2)=(
)n+(
)n=9n［(
)n+(
)2n］.
（2012•武昌区模拟）已知点P在半径为1的半圆周上沿着A→P→B路径运动，设弧 的长度为x，弓形面积为f（x）（如图所示的阴影部分），则关于函数y=f（x）的有如下结论：
的长度为x，弓形面积为f(x)(如图所示的阴影部分)，则关于函数y＝f(x)的有如下结论：
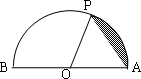
已知点P在半径为1的半圆周上沿着A→P→B路径运动，设弧 的长度为x，弓形面积为f（x）（如图所示的阴影部分），则关于函数y=f（x）的有如下结论：