题目内容
已知函数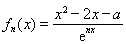 ,其中
,其中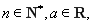
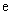 是自然对数的底数.
是自然对数的底数.
(1)求函数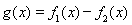 的零点;
的零点;
(2)若对任意
 均有两个极值点,一个在区间
均有两个极值点,一个在区间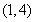 内,另一个在区间
内,另一个在区间 外,
外,
求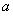 的取值范围;
的取值范围;
(3)已知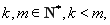 且函数
且函数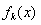 在
在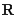 上是单调函数,探究函数
上是单调函数,探究函数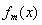 的单调性.
的单调性.
【答案】
(1)① 当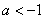 时,函数
时,函数 有1个零点:
有1个零点: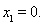 ② 当
② 当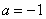 时,函数
时,函数 有2个零点:
有2个零点: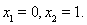 ③ 当
③ 当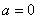 时,函数
时,函数 有两个零点:
有两个零点: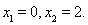 ④ 当
④ 当 时,函数
时,函数 有三个零点:
有三个零点: (2)
(2)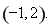 (3)探究详见解析.
(3)探究详见解析.
【解析】
试题分析:(1)令n=1,n=2,求出g(x)的表达式,在分类求出g(x)=0的解即可.
(2)对函数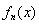 求导
求导 ,,对其分母构造函数
,,对其分母构造函数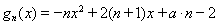 ,则
,则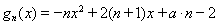 =0由有一根在
=0由有一根在 内,另一个在区间
内,另一个在区间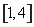 外,可得
外,可得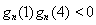 ,即
,即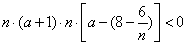 ,解出a即可.
,解出a即可.
(3)由(2)可知存在
 ,结合已知条件,可得函数
,结合已知条件,可得函数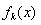 在
在 上是单调减函数, 所
上是单调减函数, 所 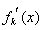 的分子的值小于等于0,其相应的判别式小于等于0,在结合已知
的分子的值小于等于0,其相应的判别式小于等于0,在结合已知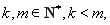 可证得
可证得
 即可.
即可.
试题解析:(1)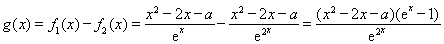 ,
,

① 当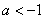 时,
时, 函数
函数 有1个零点:
有1个零点: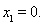 1分
1分
② 当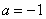 时,
时,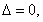 函数
函数 有2个零点:
有2个零点: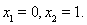 2分
2分
③ 当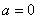 时,
时, 函数
函数 有两个零点:
有两个零点: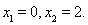 3分
3分
④ 当 时,
时, 函数
函数 有三个零点:
有三个零点:
 4分
4分
(2)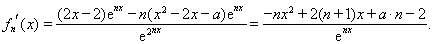 5分
5分
设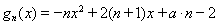 ,
, 的图像是开口向下的抛物线.
的图像是开口向下的抛物线.
由题意对任意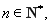
 有两个不等实数根
有两个不等实数根 ,
,
且
则对任意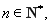
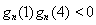 ,即
,即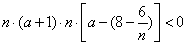 , 7分
, 7分
又任意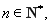
 关于
关于 递增,
递增, ,
,
故
所以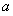 的取值范围是
的取值范围是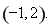 9分
9分
(3)由(2)知, 存在
 ,又函数
,又函数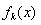 在
在 上是单调函数,故函数
上是单调函数,故函数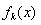 在
在 上是单调减函数, 10分
上是单调减函数, 10分
从而 即
即 11分
11分
所以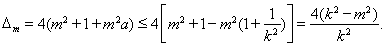
由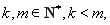 知
知 13分
13分
即对任意
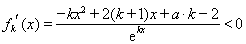
故函数 在
在 上是减函数. 14分
上是减函数. 14分
考点:1.函数的零点;2.函数的导数;3.单数性质的应用.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目






 ,其中
,其中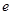 是自然对数的底数,
是自然对数的底数,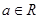 .
.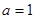 ,求曲线
,求曲线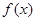 在点
在点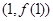 处的切线方程;
处的切线方程;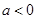 ,求
,求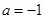 ,函数
,函数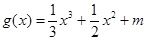 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数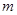 的取值范围.
的取值范围. 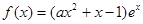 ,其中
,其中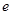 是自然对数的底数,
是自然对数的底数,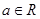 .
.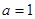 ,求曲线
,求曲线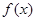 在点
在点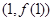 处的切线方程;
处的切线方程;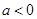 ,求
,求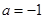 ,函数
,函数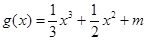 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数 的取值范围.
的取值范围.