题目内容
如图,四棱锥S-ABCD的底面是矩形,AB=a,AD=2,SA=1,且SA⊥底面ABCD,若边BC上存在异于B,C的一点P,使得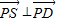 .
.(1)求a的最大值;
(2)当a取最大值时,求异面直线AP与SD所成角的大小;
(3)当a取最大值时,求平面SCD的一个单位法向量
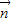 及点P到平面SCD的距离.
及点P到平面SCD的距离.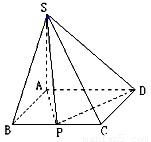
【答案】分析:首先根据题意建立空间直角坐标系,再写出各点的坐标.
(1)根据点的坐标写出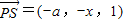 ,
,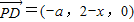 ,再由
,再由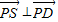 与二次函数的有关性质求出a的数值.
与二次函数的有关性质求出a的数值.
(2)分别求出两条直线所在的向量,再利用向量的有关运算求出两个向量的夹角,然后根据线线角与向量夹角的关系得到线线角.
(3)先求出平面的法向量,再求出其单位向量,然后求出平面的任意一个斜线所在的向量在法向量上的射影即可得到答案.
解答: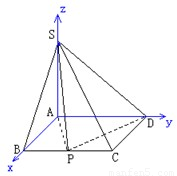 解:建立如图所示的空间直角坐标系,则各点坐标分别为:
解:建立如图所示的空间直角坐标系,则各点坐标分别为:
A(0,,0,0),B(a,0,0),C(a,2,0),D(0,2,0),S(0,0,1),设P(a,x,0).(0<x<2)
(1)∵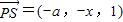 ,
,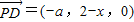
∴由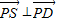 得:a2-x(2-x)=0
得:a2-x(2-x)=0
即:a2=x(2-x)(0<x<2)
∴当且仅当x=1时,a有最大值为1.此时P为BC中点;
(2)由(1)知: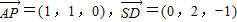 ,
,
∴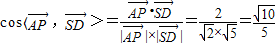 ,
,
∴异面直线AP与SD所成角的大小为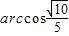 .
.
(3)设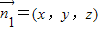 是平面SCD的一个法向量,∵
是平面SCD的一个法向量,∵ ,
,
∴由 得
得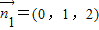 ,
,
∴平面SCD的一个单位法向量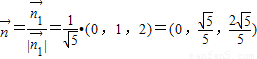 ,
,
又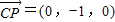 ,在
,在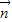 方向上的投影为
方向上的投影为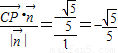 ,
,
∴点P到平面SCD的距离为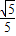 .
.
点评:本题考查线线垂直与线线角,以及点到平面的距离,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,也可以根据几何体的结构特征立空间直角坐标系利用向量的有关知识解决空间角与空间距离等问题等问题.
(1)根据点的坐标写出
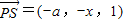 ,
,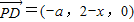 ,再由
,再由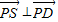 与二次函数的有关性质求出a的数值.
与二次函数的有关性质求出a的数值.(2)分别求出两条直线所在的向量,再利用向量的有关运算求出两个向量的夹角,然后根据线线角与向量夹角的关系得到线线角.
(3)先求出平面的法向量,再求出其单位向量,然后求出平面的任意一个斜线所在的向量在法向量上的射影即可得到答案.
解答:
 解:建立如图所示的空间直角坐标系,则各点坐标分别为:
解:建立如图所示的空间直角坐标系,则各点坐标分别为:A(0,,0,0),B(a,0,0),C(a,2,0),D(0,2,0),S(0,0,1),设P(a,x,0).(0<x<2)
(1)∵
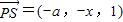 ,
,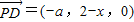
∴由
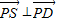 得:a2-x(2-x)=0
得:a2-x(2-x)=0即:a2=x(2-x)(0<x<2)
∴当且仅当x=1时,a有最大值为1.此时P为BC中点;
(2)由(1)知:
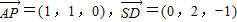 ,
,∴
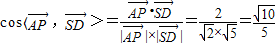 ,
,∴异面直线AP与SD所成角的大小为
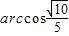 .
.(3)设
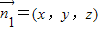 是平面SCD的一个法向量,∵
是平面SCD的一个法向量,∵ ,
,∴由
 得
得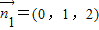 ,
,∴平面SCD的一个单位法向量
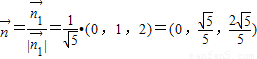 ,
,又
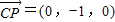 ,在
,在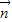 方向上的投影为
方向上的投影为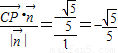 ,
,∴点P到平面SCD的距离为
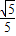 .
.点评:本题考查线线垂直与线线角,以及点到平面的距离,而空间角解决的关键是做角,由图形的结构及题设条件正确作出平面角来,是求角的关键,也可以根据几何体的结构特征立空间直角坐标系利用向量的有关知识解决空间角与空间距离等问题等问题.

练习册系列答案
相关题目
 如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC.
如图,四棱锥S-ABCD中,SD⊥底面ABCD,AB∥DC,AD⊥DC,AB=AD=1,DC=SD=2,E为棱SB上的一点,平面EDC⊥平面SBC. 如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB=
如图,四棱锥S-ABCD的底面是边长为3的正方形,SD丄底面ABCD,SB= (2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为
(2013•醴陵市模拟)如图,四棱锥S-ABCD的底面是矩形,SA⊥底面ABCD,P为BC边的中点,AD=2,AB=1.SP与平面ABCD所成角为 如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2.
如图,四棱锥S-ABCD底面ABCD是正方形,SA⊥底面ABCD,E是SC上一点,且SE=2EC,SA=6,AB=2. (2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.
(2006•西城区二模)如图,四棱锥S-ABCD中,平面SAC与底面ABCD垂直,侧棱SA、SB、SC与底面ABCD所成的角均为45°,AD∥BC,且AB=BC=2AD.