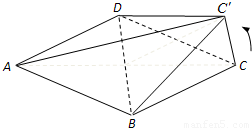
题目内容
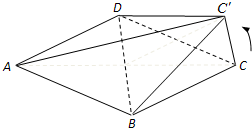 如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C′,且CC′=a(0<a<
如图,在边长为1的菱形ABCD中,将正三角形BCD沿BD向上折起,折起后的点C记为C′,且CC′=a(0<a<| 3 |
(1)若a=
| ||
| 2 |
(2)当a变化时,线段CC′上是否总存在一点E,使得AC′∥平面BED?请说明理由.
分析:(1)连接AC,交BD于点O,连接OC',菱形ABCD中,CO⊥BD,得到∠C'OC为二面角C-BD-C'的平面角,由此能求出二面角C-BD-C'的大小.
(2)当a变化时,线段CC'的中点E总满足AC'∥平面BED.因为E,O分别为线段CC',AC的中点,所以OE∥AC',所以AC'∥平面BED.
(2)当a变化时,线段CC'的中点E总满足AC'∥平面BED.因为E,O分别为线段CC',AC的中点,所以OE∥AC',所以AC'∥平面BED.
解答: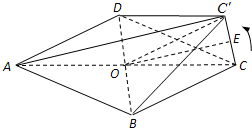 解:(1)连接AC,交BD于点O,连接OC',
解:(1)连接AC,交BD于点O,连接OC',
菱形ABCD中,CO⊥BD,
因三角形BCD沿BD折起,所以C'O⊥BD,
故∠C'OC为二面角C-BD-C'的平面角,
易得C′O=CO=
,而CC′=
,
所以∠C′OC=
,二面角C-BD-C'的大小为
;
(2)当a变化时,线段CC'的中点E总满足AC'∥平面BED,
下证之:
因为E,O分别为线段CC',AC的中点,所以OE∥AC',
又AC'?平面BED,OE?平面BED,所以AC'∥平面BED.
 解:(1)连接AC,交BD于点O,连接OC',
解:(1)连接AC,交BD于点O,连接OC',菱形ABCD中,CO⊥BD,
因三角形BCD沿BD折起,所以C'O⊥BD,
故∠C'OC为二面角C-BD-C'的平面角,
易得C′O=CO=
| ||
| 2 |
| ||
| 2 |
所以∠C′OC=
| π |
| 3 |
| π |
| 3 |
(2)当a变化时,线段CC'的中点E总满足AC'∥平面BED,
下证之:
因为E,O分别为线段CC',AC的中点,所以OE∥AC',
又AC'?平面BED,OE?平面BED,所以AC'∥平面BED.
点评:本题主要考查直线与平面、平面与平面的位置关系,考查空间想象、推理论证能力.

练习册系列答案
 巧学巧练系列答案
巧学巧练系列答案
相关题目
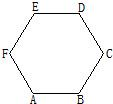
如图,在边长为1的正六边形ABCDEF中,下列向量的数量积中最大的是( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
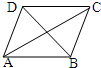 如图,在边长为1的棱形ABCD中,AC2+BD2=
如图,在边长为1的棱形ABCD中,AC2+BD2=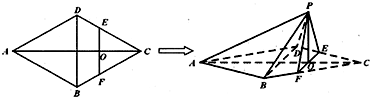
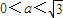 ).
).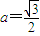 ,求二面角C-BD-C′的大小;
,求二面角C-BD-C′的大小;