题目内容
(本小题满分14分)
已知函数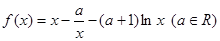 .
.
(Ⅰ)当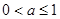 时,求函数
时,求函数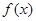 的单调区间;
的单调区间;
(Ⅱ)是否存在实数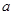 ,使
,使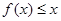 恒成立,若存在,求出实数
恒成立,若存在,求出实数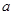 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
已知函数
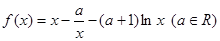 .
.(Ⅰ)当
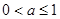 时,求函数
时,求函数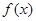 的单调区间;
的单调区间;(Ⅱ)是否存在实数
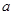 ,使
,使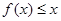 恒成立,若存在,求出实数
恒成立,若存在,求出实数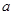 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.(Ⅰ)(1)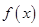 的单调增区间为
的单调增区间为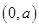 和
和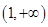 ,单调减区间为
,单调减区间为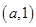
(2)当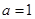 时,
时, 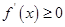 ,
,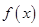 的单调增区间为
的单调增区间为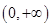
(Ⅱ) 时,使
时,使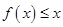 恒成立.
恒成立.
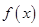 的单调增区间为
的单调增区间为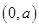 和
和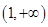 ,单调减区间为
,单调减区间为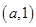
(2)当
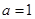 时,
时, 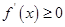 ,
,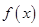 的单调增区间为
的单调增区间为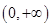
(Ⅱ)
 时,使
时,使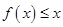 恒成立.
恒成立. (1)先求出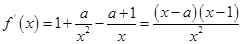 ,根据定义域
,根据定义域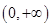 ,然后讨论对a进行讨论确定单调区间。
,然后讨论对a进行讨论确定单调区间。
(2)解本题的关键是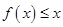 恒成立可转化为
恒成立可转化为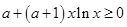 恒成立,
恒成立,
令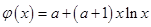 ,则只需
,则只需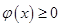 在
在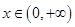 恒成立即可.然后再利用导数研究其最值,问题得解。
恒成立即可.然后再利用导数研究其最值,问题得解。
解:(Ⅰ)函数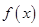 的定义域为
的定义域为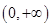 ,
,
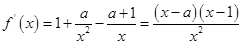 …………………………2分
…………………………2分
(1)当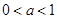 时,由
时,由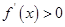 得,
得,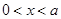 或
或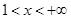 ,由
,由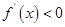 得,
得,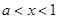
故函数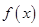 的单调增区间为
的单调增区间为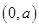 和
和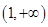 ,单调减区间为
,单调减区间为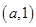 …………4分
…………4分
(2)当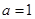 时,
时, 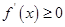 ,
,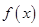 的单调增区间为
的单调增区间为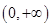 …………………………5分
…………………………5分
(Ⅱ)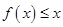 恒成立可转化为
恒成立可转化为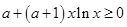 恒成立,
恒成立,
令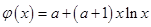 ,则只需
,则只需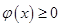 在
在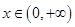 恒成立即可,………6分
恒成立即可,………6分
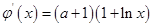
当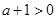 时,在
时,在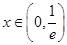 时,
时,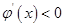 ,在
,在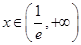 时,
时,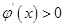
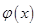 的最小值为
的最小值为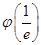 ,由
,由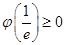 得
得 ,
,
故当 时
时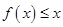 恒成立, ……………………………………9分
恒成立, ……………………………………9分
当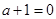 时,
时,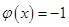 ,
,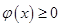 在
在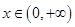 不能恒成立,……………11分
不能恒成立,……………11分
当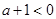 时,取
时,取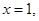 有
有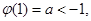
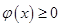 在
在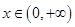 不能恒成立,…13分
不能恒成立,…13分
综上所述当 时,使
时,使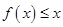 恒成立. ………………………14分
恒成立. ………………………14分
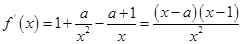 ,根据定义域
,根据定义域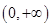 ,然后讨论对a进行讨论确定单调区间。
,然后讨论对a进行讨论确定单调区间。(2)解本题的关键是
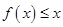 恒成立可转化为
恒成立可转化为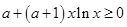 恒成立,
恒成立,令
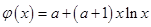 ,则只需
,则只需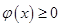 在
在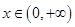 恒成立即可.然后再利用导数研究其最值,问题得解。
恒成立即可.然后再利用导数研究其最值,问题得解。解:(Ⅰ)函数
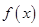 的定义域为
的定义域为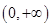 ,
,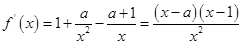 …………………………2分
…………………………2分(1)当
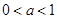 时,由
时,由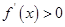 得,
得,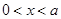 或
或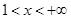 ,由
,由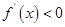 得,
得,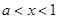
故函数
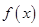 的单调增区间为
的单调增区间为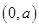 和
和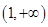 ,单调减区间为
,单调减区间为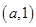 …………4分
…………4分(2)当
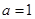 时,
时, 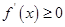 ,
,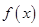 的单调增区间为
的单调增区间为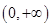 …………………………5分
…………………………5分(Ⅱ)
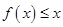 恒成立可转化为
恒成立可转化为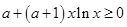 恒成立,
恒成立,令
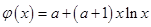 ,则只需
,则只需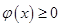 在
在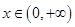 恒成立即可,………6分
恒成立即可,………6分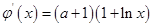
当
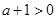 时,在
时,在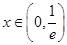 时,
时,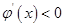 ,在
,在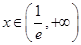 时,
时,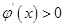
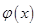 的最小值为
的最小值为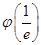 ,由
,由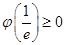 得
得 ,
,故当
 时
时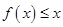 恒成立, ……………………………………9分
恒成立, ……………………………………9分当
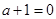 时,
时,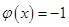 ,
,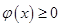 在
在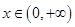 不能恒成立,……………11分
不能恒成立,……………11分当
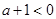 时,取
时,取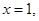 有
有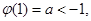
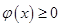 在
在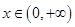 不能恒成立,…13分
不能恒成立,…13分综上所述当
 时,使
时,使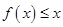 恒成立. ………………………14分
恒成立. ………………………14分
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
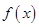 在
在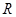 上的导函数为
上的导函数为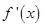 ,且
,且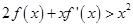 ,下面的不等式在
,下面的不等式在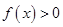
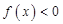

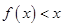
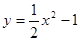 在点
在点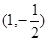 处切线的倾斜角为( )
处切线的倾斜角为( )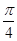


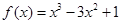 在
在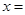 处取得极小值.
处取得极小值.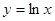 在点
在点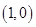 处的切线方程为________.
处的切线方程为________. 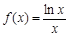 单调增区间是 ;
单调增区间是 ;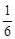 处的切线的倾斜角是
处的切线的倾斜角是 π
π
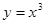 在点
在点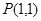 的切线方程为 .
的切线方程为 .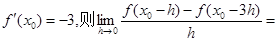 ___________.
___________.