题目内容
设各项为正数的等比数列{an}的前n项和为Sn,S4=1,S8=17.(Ⅰ)求数列{an}的通项公式;
(Ⅱ)是否存在最小正整数m,使得当n>m时,an<
| 2011 | 15 |
分析:(Ⅰ)由S4=1,S8=17,得到公比q不等于1,所以根据等比数列的前n项和公式化简两等式,得到关于首项和公比的两方程,两方程相除即可消去首项,求出公比的值,把公比的值代入其中一个方程即可求出首项的值,由首项和公比的值写出数列的通项公式即可;
(Ⅱ)把(Ⅰ)中求出的通项公式代入an<
中,化简后根据2011的范围把2011夹在2的11次方和2的12次方之间,即可求出不存在n的最小正整数解,使n大于此时的最小正整数时不等式恒成立.
(Ⅱ)把(Ⅰ)中求出的通项公式代入an<
| 2011 |
| 15 |
解答:解:(Ⅰ)设数列{an}的公比为q,由S4=1,S8=17知q≠1,
则
=1,
=17,相除得:
=17,解得q4=16,所以q=2或q=-2(舍去),
将q=2代入得a1=
,则数列{an}的通项公式为an=
;
(Ⅱ)由an=
<
,得2n-1<2011,
而210<2011<211,所以n-1≤10,即n≤11,
因此,不存在最小的正整数,使得n≥m时,an>
恒成立.
则
| a1(1-q4) |
| 1-q |
| a1(1-q8) |
| 1-q |
| 1-q8 |
| 1-q4 |
将q=2代入得a1=
| 1 |
| 15 |
| 2n-1 |
| 15 |
(Ⅱ)由an=
| 2n-1 |
| 15 |
| 2011 |
| 15 |
而210<2011<211,所以n-1≤10,即n≤11,
因此,不存在最小的正整数,使得n≥m时,an>
| 2011 |
| 15 |
点评:此题考查学生灵活运用等比数列的前n项和公式及通项公式化简求值,掌握不等式恒成立时满足的条件,是一道中档题.

练习册系列答案
相关题目
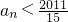 恒成立?若存在,求出m;若不存在,请说明理由.
恒成立?若存在,求出m;若不存在,请说明理由.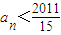 恒成立?若存在,求出m;若不存在,请说明理由.
恒成立?若存在,求出m;若不存在,请说明理由.