题目内容
19.在平面直角坐标系中,A(1,t),C(-2t,2),$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OC}$(O是坐标原点),其中t∈(0,+∞).(1)求 B点坐标;
(2)求四边形OABC在第一象限部分的面积S(t).
分析 (1)根据向量的坐标运算即可求B点坐标;
(2)根据条件判断四边形OABC为矩形,然后根据B的坐标求出四边形OABC在第一象限部分图象即可得到结论.
解答 解:(1)∵A(1,t),C(-2t,2),
∴$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OC}$=(1,t)+(-2t,2)=(1-2t,t+2),
即B(1-2t,t+2).
(2)∵$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OC}$,∴OABC为平行四边形,
又∵$\overrightarrow{OA}•\overrightarrow{OC}=-2t+2t=0$,
∴OA⊥OC,∴四边形OABC为矩形.
∵$\overrightarrow{OB}=\overrightarrow{OA}+\overrightarrow{OC}$=(1-2t,t+2),
当1-2t>0,即0<t<$\frac{1}{2}$时,
A在第一象限,B在第一象限,C在第二象限,(如图1)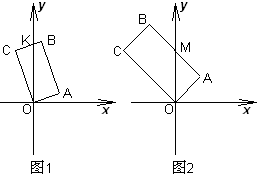
此时BC的方程为:y-2=t(x+2t),
令x=0,得BC交y轴于K(0,2t2+2),
∴S(t)=SOABC-S△OKC=2(1-t+t2-t3)=2(-t3+t2-t+1).
当1-2t≤0,即t≥$\frac{1}{2}$时,A在第一象限,B在y轴上或在第二象限,C在第二象限,(如图2)
此时AB的方程为:y-t=-$\frac{1}{t}$(x-1),
令x=0,得AB交轴于M(0,t+$\frac{1}{t}$),
∴S(t)=S△OAM=$\frac{1}{2}$(t+$\frac{1}{t}$),
∴S(t)=$\left\{\begin{array}{l}{2(-{t}^{3}+{t}^{2}-t+1),}&{0<t<\frac{1}{2}}\\{\frac{1}{2}(t+\frac{1}{t}),}&{t≥\frac{1}{2}}\end{array}\right.$.
点评 本题主要考查平面向量坐标的基本运算,以及平面向量的应用,综合性较强,根据条件判断四边形OABC为矩形是解决本题的关键..

 如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )
如图,四棱锥S-ABCD的底面为正方形,SD⊥底面ABCD,则下列结论中不正确的是( )| A. | AC⊥SB | |
| B. | AB∥平面SCD | |
| C. | AC⊥面SBD | |
| D. | AB与SC所成的角等于DC与SA所成的角 |
| A. | $\frac{8-π}{4}$ | B. | $\frac{4-π}{4}$ | C. | $\frac{2-π}{2}$ | D. | $\frac{4-π}{8}$ |
 如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,BC=4,AB=PA=2,M为线段PC的中点,N在线段BC上,且BN=1.
如图,四棱锥P-ABCD的底面ABCD为矩形,PA⊥底面ABCD,BC=4,AB=PA=2,M为线段PC的中点,N在线段BC上,且BN=1.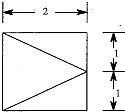 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.
已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为$\frac{4}{3}$.