题目内容
定义:关于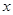 的不等式
的不等式 的解集叫
的解集叫 的
的 邻域.已知
邻域.已知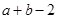 的
的 邻域为区间
邻域为区间 ,其中
,其中 、
、 分别为椭圆
分别为椭圆 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线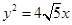 的焦点重合,则椭圆的方程为( )
的焦点重合,则椭圆的方程为( )
A. | B.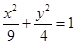 | C. | D.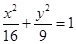 |
B
解析试题分析:由题中的定义知,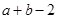 的
的 邻域为区间
邻域为区间 ,则关于
,则关于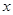 不等式
不等式 的解集为
的解集为 ,解关于
,解关于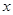 不等式
不等式 得
得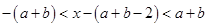 ,解得
,解得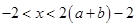 ,所以
,所以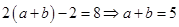 ,又由于椭圆
,又由于椭圆 的一焦点与抛物线
的一焦点与抛物线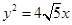 的焦点
的焦点 重合,则
重合,则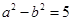 ,即
,即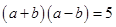 ,所以
,所以 ,解得
,解得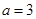 ,
, ,
,
故此椭圆的方程为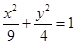 ,故选B.
,故选B.
考点:1.新定义;2.含绝对值的不等式的解法;3.椭圆的方程

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
已知一元二次不等式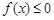 的解集为
的解集为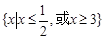 ,则
,则 的解集为( )
的解集为( )
A.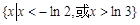 | B.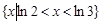 |
C.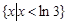 } } | D. |
已知集合 ,则
,则 ( )
( )
A. | B.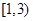 | C. | D. |
已知
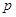 是
是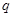 的充分条件,则实数
的充分条件,则实数 的取值范围是( )
的取值范围是( )
A.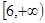 | B.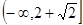 | C. | D. |
若关于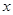 的不等式
的不等式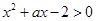 在区间
在区间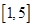 上有解,则实数
上有解,则实数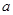 的取值范围为 ( )
的取值范围为 ( )
A.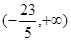 | B.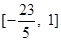 | C.(1,+∞) | D.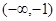 |
若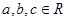 ,且
,且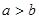 ,则下列不等式一定成立的是 ( )
,则下列不等式一定成立的是 ( )
A.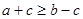 | B.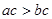 |
C.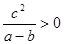 | D.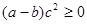 |
不等式ax2+bx+2>0的解集是 ,则a+b的值是( )
,则a+b的值是( )
| A.10 | B.-10 |
| C.-14 | D.14 |
设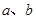 是互不相等的正数,则下列不等式中不恒成立的是( )
是互不相等的正数,则下列不等式中不恒成立的是( )
A.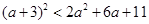 | B.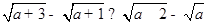 |
C.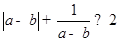 | D.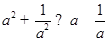 |
若不等式|8x+9|<7和不等式ax2+bx>2的解集相等,则实数a、b的值分别为( )
| A.a=-8,b=-10 |
| B.a=-4,b=-9 |
| C.a=-1,b=9 |
| D.a=-1,b=2 |