题目内容
设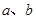 是互不相等的正数,则下列不等式中不恒成立的是( )
是互不相等的正数,则下列不等式中不恒成立的是( )
A.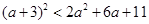 | B.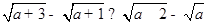 |
C.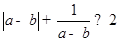 | D.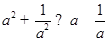 |
C
解析试题分析: 恒成立,所以A正确;因为
恒成立,所以A正确;因为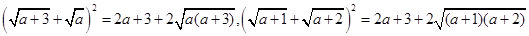 ,所以
,所以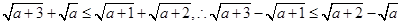 恒成立,所以B正确;而
恒成立,所以B正确;而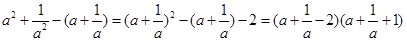 ,因为
,因为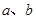 是互不相等的正数,所以上式恒成立,所以D正确;当
是互不相等的正数,所以上式恒成立,所以D正确;当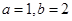 时,C不恒成立,所以C不正确.
时,C不恒成立,所以C不正确.
考点:本小题主要考查不等式的性质和应用,基本不等式的应用等.
点评:解决此类问题,要注意各个性质的适用条件,比如基本不等式就要注意“一正二定三相等”三个条件缺一不可.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
若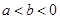 ,则下列不等式:①
,则下列不等式:①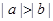 ;②
;② ;③
;③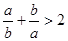 ;④
;④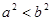 中,正确的有( )
中,正确的有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
要使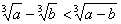 成立,则
成立,则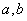 应满足的条件是
应满足的条件是
A.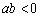 且 且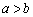 | B.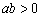 且 且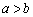 |
C.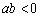 且 且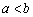 | D.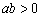 且 且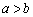 或 或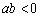 且 且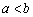 |
若关于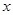 的不等式
的不等式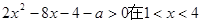 内有解,则实数
内有解,则实数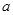 的取值范围是( )
的取值范围是( )
A.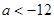 | B.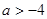 | C.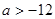 | D.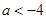 |
不等式│3-x│<2的解集是 ( ).
| A.{x│x>5或x<1} | B.{x│1<x<5} | C.{x│-5<x<-1} | D.{x│x>1} |
不等式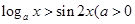 且
且 对任意
对任意 都成立,则
都成立,则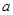 的取值
的取值
范围为
A.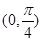 | B. | C.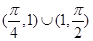 | D.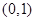 |
若不等式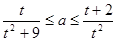 在
在 上恒成立,则
上恒成立,则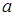 的取值范围是( )
的取值范围是( )
A.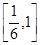 | B.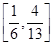 | C.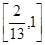 | D.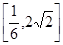 |
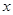 的不等式
的不等式 的解集叫
的解集叫 的
的 邻域.已知
邻域.已知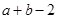 的
的 邻域为区间
邻域为区间 ,其中
,其中 、
、 分别为椭圆
分别为椭圆 的长半轴和短半轴.若此椭圆的一焦点与抛物线
的长半轴和短半轴.若此椭圆的一焦点与抛物线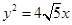 的焦点重合,则椭圆的方程为( )
的焦点重合,则椭圆的方程为( )
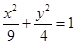

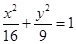
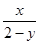 ,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )
,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )