题目内容
((本小题满分10分)选修4—1:几何证明选讲
自圆O外一点P引圆的一条切线PA,切点为A,M为PA的中点,过点M引圆O的割线交该圆于B、C两点,且∠BMP=100°,∠BPC=40°,求∠MPB的大小。
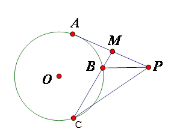
自圆O外一点P引圆的一条切线PA,切点为A,M为PA的中点,过点M引圆O的割线交该圆于B、C两点,且∠BMP=100°,∠BPC=40°,求∠MPB的大小。

解:因为MA是圆O的切线,所以MA2=MB·MC………………………………………… …2分
…2分
又M是PA的中点,所以MP2=MB·MC
因为∠BMP=∠PMC,所以△BMP∽△PMC……………………………………………………6分
于是∠MPB=∠MCP,
在△MCP中,由∠MPB+∠MCP+∠BPC+∠BMP =180°,得∠MPB=20°…………………10分
 …2分
…2分又M是PA的中点,所以MP2=MB·MC
因为∠BMP=∠PMC,所以△BMP∽△PMC……………………………………………………6分
于是∠MPB=∠MCP,
在△MCP中,由∠MPB+∠MCP+∠BPC+∠BMP =180°,得∠MPB=20°…………………10分
略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
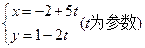 与坐标轴的交点是( )
与坐标轴的交点是( )




 B.1 C.2
B.1 C.2 中,
中,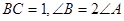 ,则
,则 的取值范围是( )
的取值范围是( )



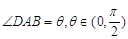 ,以A,B为焦点且过点D的双曲线离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( )
,以A,B为焦点且过点D的双曲线离心率为e1,以C,D为焦点且过点A的椭圆的离心率为e2,则( ) 角增大,e1增大,e1 e2为定值
角增大,e1增大,e1 e2为定值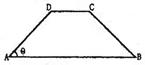
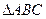 中,
中,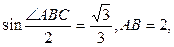
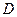 在线
在线 段
段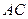 上,且
上,且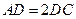 ,
,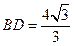
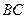 的长;
的长;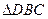 的面积.
的面积.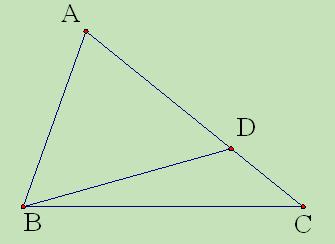
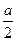 ,点E,F分别为线段AB,CD的中点,则EF= .
,点E,F分别为线段AB,CD的中点,则EF= .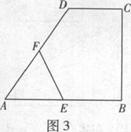
 的中点
的中点 ,P是直径MN上一动点,圆的半径为1,则PA+PB的最小值为 。
,P是直径MN上一动点,圆的半径为1,则PA+PB的最小值为 。