题目内容
如图已知四棱锥P—ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB∥CD,AB=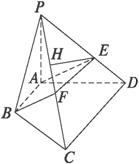
(1)点F在线段PC上运动,且设![]() =λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
=λ,问当λ为何值时,BF∥平面PAD?并证明你的结论;
(2)二面角F—CD—B为45°,求二面角B—PC—D的大小;
(3)在(2)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
解:(1)当λ=1时,BF∥平面PAD.

证明:取PD中点E,则EF∥CD,
且EF=![]() CD,又AB∥CD且AB=
CD,又AB∥CD且AB=![]() CD,
CD,
![]() ∴四边形ABFE为平行四边形.
∴四边形ABFE为平行四边形.
∴BF∥AE.又AE![]() 平面PAD,
平面PAD,
∴BF∥平面PAD.
(2)∵PA⊥平面ABCD,CD⊥AD,
CD⊥PD,∠PDA即是二面角的平面角∠PDA=45°,
∴△PAD为等腰直角三角形,∴AE⊥PD,∵CD⊥AD,∴AE⊥CD,
∴AE⊥平面PCD.
又BF∥AE,
∴BF⊥平面PCD.∵BF![]() 平面PBC,
平面PBC,
∴平面PCD⊥平面PBC,即二面角B—PC—D的大小为90°.
(3)在平面PCD内作EH⊥PC于点H,由平面PCD⊥平面PBC且平面PCD∩平面PBC=PC知:EH⊥平面PBC.
在Rt△PCD中,PC=![]() ,
,
在Rt△PEF 中,EH·PF=PE·EF,将PE=![]() ,PF=
,PF=![]() ,EF=
,EF=![]() 代入得
代入得
EH=![]() .即点E到平面PBC的距离为
.即点E到平面PBC的距离为![]() .
.
又∵AE∥BF,∴AE∥平面PBC,
∴点A到平面PBC的距离为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1.
如图,已知四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥DC,∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1. 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知 如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AD=a,
如图,已知四棱锥P-ABCD的底面ABCD是平行四边形,PA=AB=AD=a,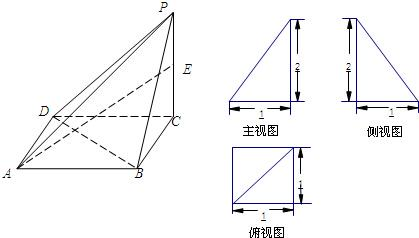 (2010•广东模拟)已知四棱锥P-ABCD的三视图如图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.
(2010•广东模拟)已知四棱锥P-ABCD的三视图如图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.E是侧棱PC上的动点.