题目内容
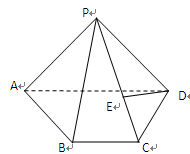
如图1,在平行四边形ABCD中,AB=1,BD=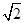 ,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
,∠ABD=90°,E是BD上的一个动点,现将该平行四边形沿对角线BD折成直二面角A-BD-C,如图2所示.
(1)若F、G分别是AD、BC的中点,且AB∥平面EFG,求证:CD∥平面EFG;
(2)当图1中AE+EC最小时,求图2中二面角A-EC-B的大小.
(1)只需证CD//EG;(2)60°。
解析试题分析:(1)证明(略) 4分
(2)由图1可知,当AE+EC最小时,E是BD的中点
∵平面ABD⊥平面BCD,AB⊥BD,∴AB⊥面BCD.
故以B为坐标原点,平行于CD的直线为x轴,
BD所在的直线为y轴,AB所在的直线为z轴,建立
如图所示空间直角坐标系B-xyz.
则A(0,0,1),C(1,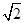 ,0),D(0
,0),D(0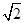 ,0),E(0,
,0),E(0,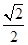 ,0)
,0)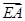 =(0,-
=(0,-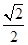 ,1),
,1),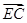 =(1,
=(1,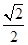 ,0)
,0)
设平面AEC的一个法向量为n1=(x,y,z)
则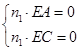 Þ
Þ 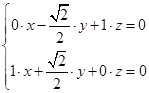
解得x=-z,y=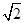 z
z
∴平面AEC的一个法向量为n1=(-1,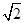 ,1)
,1)
而平面BCE的一个法向量为n2=(0,0,1)
∴cos<n1,n2> =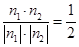 10'
10'
显然,二面角A-EC-B为锐角,所以,二面角A-EC-B的大小为60°. 12分
考点:线面平行的性质定理;线面垂直的判定定理;二面角。
点评:二面角的求法是立体几何中的一个难点。我们解决此类问题常用的方法有两种:①综合法,综合法的一般步骤是:一作二说三求。②向量法,运用向量法求二面角应注意的是计算。很多同学都会应用向量法求二面角,但结果往往求不对,出现的问题就是计算错误。

练习册系列答案
相关题目
 ABC=60
ABC=60 ,EC
,EC 面ABCD,FA
面ABCD,FA
 ,面
,面 ⊥面
⊥面 .侧面
.侧面 为直角顶点的等腰直角三角形,底面
为直角顶点的等腰直角三角形,底面 ,
, ∥
∥ ,
, ⊥
⊥ 为
为 上一点,且
上一点,且 .
.
 ⊥
⊥ ;
; 的正弦值.
的正弦值. 中,
中, ,
, ,
, .
. 
 平面
平面 ;
; ,且异面直线
,且异面直线 与
与 的夹角为
的夹角为 时,求二面角
时,求二面角 的余弦值.
的余弦值. ,VA =" 6."
,VA =" 6." 
 ,F是BC的中点.
,F是BC的中点.
 ,
, ,
,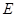 是
是 的中点,
的中点, 是
是 中点.
中点.
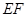 ∥面
∥面 ;
;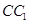 所成角的正切值;
所成角的正切值;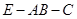 的平面角为
的平面角为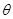 ,求
,求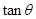 的值.
的值. 中,
中,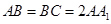
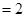 ,
, ,
, 是
是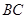 的中点.
的中点.
 平行平面
平行平面 ;
; 的余弦值;
的余弦值;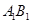 上是否存在点
上是否存在点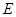 ,使
,使 与
与 成
成 角?若存在,确定
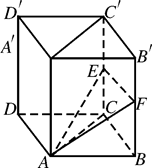
角?若存在,确定 ,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.
,E、F分别是棱CC′与BB′上的点,且EC=BC=2FB=2.