题目内容
(2012•湖北模拟)某日,我渔政船在东海某海域巡航,已知该船正以30(
-1)海里/时的速度向正北方向航行,该船在A点处发现北偏东30°方向的海面上有一个小岛,继续航行20分钟到达B点,发现该小岛在北偏东45°方向上,若该船向北继续航行,船与小岛的最小距离可以达到( )海里.
| 3 |
分析:根据题意画出相应的图形,过C作CD垂直于AD,垂足为D,将20分钟化为小时,乘以速度求出AB的距离,由∠A的度数求出∠ACD的度数,由∠DBC=45°,得到三角形BDC为等腰直角三角形,可设CD=BD=x,由AD=AB+DB表示出AD,在三角形ACD中,利用正弦定理列出方程,求出方程的解得到x的值,即为船与小岛的最小距离.
解答: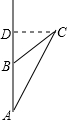 解:根据题意画出相应的图形,如图所示,过C作CD⊥AD,
解:根据题意画出相应的图形,如图所示,过C作CD⊥AD,
由题意得:AB=
×30(
-1)=10(
-1)(海里),
∵∠A=30°,∴∠ACD=60°,
由∠DBC=45°,得到△DBC为等腰直角三角形,
设CD=BD=x海里,AD=AB+BD=x+10(
-1)(海里),
在△ACD中,由正弦定理得:
=
,
即
=
,
解得:x=10,
则该船向北继续航行,船与小岛的最小距离可以达到10海里.
故选C
 解:根据题意画出相应的图形,如图所示,过C作CD⊥AD,
解:根据题意画出相应的图形,如图所示,过C作CD⊥AD,由题意得:AB=
| 20 |
| 60 |
| 3 |
| 3 |
∵∠A=30°,∴∠ACD=60°,
由∠DBC=45°,得到△DBC为等腰直角三角形,
设CD=BD=x海里,AD=AB+BD=x+10(
| 3 |
在△ACD中,由正弦定理得:
| AD |
| sin∠ACD |
| CD |
| sinA |
即
x+10(
| ||||
|
| x | ||
|
解得:x=10,
则该船向北继续航行,船与小岛的最小距离可以达到10海里.
故选C
点评:此题考查了正弦定理,属于解三角形的题型,熟练掌握正弦定理是解本题的关键.

练习册系列答案
相关题目
 (2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=
(2012•湖北模拟)已知函数y=g(x)的图象由f(x)=sin2x的图象向右平移φ(0<φ<π)个单位得到,这两个函数的部分图象如图所示,则φ=