题目内容
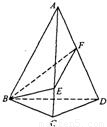
如图,已知在三棱锥D—ABC中,DA⊥面ABC,且AB=BC=AD=1,∠ABC=90°,求二面角A—CD—B的大小.
分析:用向量法和向量坐标法解答本题.

解:以B为原点,BC,BA所在的直线分别为x,y轴,过B平行于AD的直线为z轴,建立空间直角坐标系,则B(0,0,0),A(0,1,0),C(1,0,0),D(0,1,1).
作AE⊥CD,BF⊥CD,E,F为垂足,AD=1,AC=![]() ,DC=
,DC=![]() ,由射影定理,得
,由射影定理,得
DE=![]() ,CF=
,CF=![]() ,则
,则
E(![]() ,
,![]() ,
,![]() ),F(
),F(![]() ,
,![]() ,
,![]() ),
),![]() =(
=(![]() ,-
,-![]() ,
,![]() ),
),![]() =(
=(![]() ,
,![]() ,
,![]() ),
),![]() ·
·![]() =
=![]() .
.
又|![]() |=|
|=|![]() |=
|=![]() ,
,
cos〈![]() ,
,![]() 〉=
〉=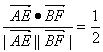 ,
,
即二面角A—CD—B的大小为60°.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目