题目内容
已知向量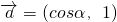 ,
,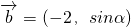 ,
,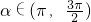 ,且
,且 .
.
(Ⅰ)求sinα的值;
(Ⅱ)求tan2α的值.
解:(Ⅰ)由向量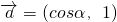 ,
,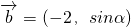 ,且
,且 .
.
可得 =(cosα,1)•(-2,sinα)=0.
=(cosα,1)•(-2,sinα)=0.
即-2cosα+sinα=0. 所以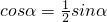 .(3分)
.(3分)
因为sin2α+cos2α=1,所以 .
.
因为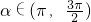 ,所以
,所以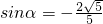 .(7分)
.(7分)
(Ⅱ)由(Ⅰ)可得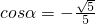 .
.
再由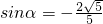 ,则得 tanα=2.(8分)
,则得 tanα=2.(8分)
故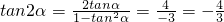 .(13分)
.(13分)
分析:(Ⅰ)由 两个向量垂直的性质建立方程可求得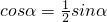 ,再由同角三角函数的基本关系及角α的范围求出
,再由同角三角函数的基本关系及角α的范围求出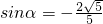 ,
,
(Ⅱ)由(Ⅰ)可得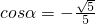 ,利用同角三角函数的基本关系求出
,利用同角三角函数的基本关系求出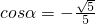 ,进而求得tanα的值,再由二倍角公式求出tan2α的值.
,进而求得tanα的值,再由二倍角公式求出tan2α的值.
点评:本题主要考查两个向量的数量积公式的应用,两个向量垂直的性质,同角三角函数的基本关系和二倍角公式的应用,属于中档题.
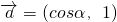 ,
,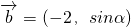 ,且
,且 .
.可得
 =(cosα,1)•(-2,sinα)=0.
=(cosα,1)•(-2,sinα)=0.即-2cosα+sinα=0. 所以
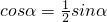 .(3分)
.(3分)因为sin2α+cos2α=1,所以
 .
.因为
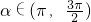 ,所以
,所以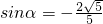 .(7分)
.(7分)(Ⅱ)由(Ⅰ)可得
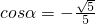 .
.再由
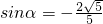 ,则得 tanα=2.(8分)
,则得 tanα=2.(8分)故
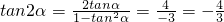 .(13分)
.(13分)分析:(Ⅰ)由 两个向量垂直的性质建立方程可求得
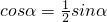 ,再由同角三角函数的基本关系及角α的范围求出
,再由同角三角函数的基本关系及角α的范围求出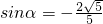 ,
,(Ⅱ)由(Ⅰ)可得
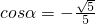 ,利用同角三角函数的基本关系求出
,利用同角三角函数的基本关系求出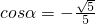 ,进而求得tanα的值,再由二倍角公式求出tan2α的值.
,进而求得tanα的值,再由二倍角公式求出tan2α的值.点评:本题主要考查两个向量的数量积公式的应用,两个向量垂直的性质,同角三角函数的基本关系和二倍角公式的应用,属于中档题.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
已知向量
,
且
=
+2
,
=-5
+6
=7
-2
,则一定共线的三点是( )
. |
| a |
| b |
| AB |
| a |
| b |
| BC |
| a |
| b, |
| CD |
| a |
| b |
| A、A、B、D |
| B、A、B、C |
| C、A、C、D |
| D、B、C、D |
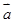 ,
,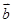 的夹角为
的夹角为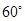 , 且
, 且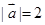 ,
, 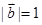 ,
若
,
若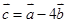 ,
, 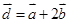 求:
(1)
求:
(1) 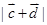 .
.
 ,函数
,函数 ,且
,且 图
图 象上一个最高点的坐标为
象上一个最高点的坐标为 ,与之相邻
,与之相邻 的一个最低点的坐标为
的一个最低点的坐标为 .
. 是角A、B、C所对的边,且满足
是角A、B、C所对的边,且满足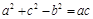 ,求角B的大
,求角B的大 的取值范围.
的取值范围.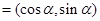 ,b
,b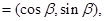 且a,b满足|ka+b |=
且a,b满足|ka+b |=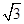 |a-kb|
|a-kb|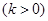 ,
,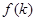 ;
;