题目内容
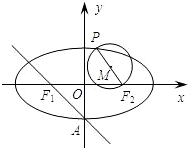 已知椭圆C:
已知椭圆C:| x2 |
| 2 |
(Ⅰ)当⊙M的面积为
| π |
| 8 |
(Ⅱ)当⊙M与直线AF1相切时,求⊙M的方程;
(Ⅲ)求证:⊙M总与某个定圆相切.
分析:(Ⅰ)根据椭圆方程求得焦点,顶点的坐标,设出点P的坐标,进而表示出|PF2|的长度进而根据圆M的面积求得x1,求得P的坐标,则PA所在的直线方程可得.
(Ⅱ)根据点M到直线AF1的距离求得x1和y1的关系式,进而与椭圆方程联立求得x1,进而求得M的坐标则圆的方程可得.
(Ⅲ)首先表示出OM的长度,以及圆M的半径,进而求得OM=r1-r2,推断出⊙M和以原点为圆心,半径为r1=
(长半轴)的圆相内切.
(Ⅱ)根据点M到直线AF1的距离求得x1和y1的关系式,进而与椭圆方程联立求得x1,进而求得M的坐标则圆的方程可得.
(Ⅲ)首先表示出OM的长度,以及圆M的半径,进而求得OM=r1-r2,推断出⊙M和以原点为圆心,半径为r1=
| 2 |
解答:解:(Ⅰ)易得F1(-1,0),F2(1,0),A(0,-1),设点P(x1,y1),
则PF22=(x1-1)2+y12=(x1-1)2+1-
=
(x1-2)2,
所以PF2=
-
x1
又⊙M的面积为
,∴
=
(x1-2)2,
解得x1=1,∴P(1,
)或(1,-
),
∴PA所在直线方程为y=(1+
)x-1或y=(1-
)x-1
(Ⅱ)因为直线AF1的方程为x+y+1=0,且M(
,
)到直线AF1的距离为
=
-
x1
化简得y1=-1-2x1,联立方程组
,
解得x1=0或x1=-
∴当x1=0时,可得M(
,-
),
∴⊙M的方程为(x-
)2+(y+
)2=
;
当x1=-
时,可得M(
,
),
∴⊙M的方程为(x-
)2+(y-
)2=
(Ⅲ)⊙M始终和以原点为圆心,半径为r1=
(长半轴)的圆(记作⊙O)相切
证明:因为OM=
=
=
+
x1,
又⊙M的半径r2=MF2=
-
x1,
∴OM=r1-r2,∴⊙M和⊙O相内切.
则PF22=(x1-1)2+y12=(x1-1)2+1-
| x12 |
| 2 |
| 1 |
| 2 |
所以PF2=
| 2 |
| ||
| 2 |
又⊙M的面积为
| π |
| 8 |
| π |
| 8 |
| π |
| 8 |
解得x1=1,∴P(1,
| ||
| 2 |
| ||
| 2 |
∴PA所在直线方程为y=(1+
| ||
| 2 |
| ||
| 2 |
(Ⅱ)因为直线AF1的方程为x+y+1=0,且M(
| x1+1 |
| 2 |
| y1 |
| 2 |
|
| ||||
|
| ||
| 2 |
| ||
| 4 |
化简得y1=-1-2x1,联立方程组
|
解得x1=0或x1=-
| 8 |
| 9 |
∴当x1=0时,可得M(
| 1 |
| 2 |
| 1 |
| 2 |
∴⊙M的方程为(x-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
当x1=-
| 8 |
| 9 |
| 1 |
| 18 |
| 7 |
| 18 |
∴⊙M的方程为(x-
| 1 |
| 18 |
| 7 |
| 18 |
| 169 |
| 162 |
(Ⅲ)⊙M始终和以原点为圆心,半径为r1=
| 2 |
证明:因为OM=
|
=
|
| ||
| 2 |
| ||
| 4 |
又⊙M的半径r2=MF2=
| ||
| 2 |
| ||
| 4 |
∴OM=r1-r2,∴⊙M和⊙O相内切.
点评:本题主要考查了直线与圆锥曲线的综合问题.直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.

练习册系列答案
相关题目