题目内容
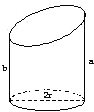 如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是
如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是分析:用补形法:两个相同的几何体,倒立一个,对应合缝,恰好形成一个圆柱体.求出总体积的一半即可.
解答:解:取两个相同的几何体,倒立一个,对应合缝,恰好形成一个圆柱体.
所求几何体的体积:
×πr2×(a+b)=
πr2(a+b)
故答案为:
πr2(a+b)
所求几何体的体积:
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查几何体的体积,考查转化思想,是基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
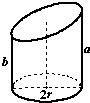
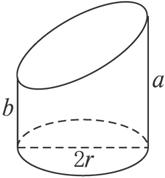
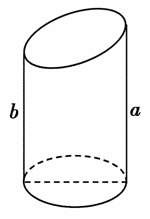
 如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是 .
如图,已知底面半径为r的圆柱被一个平面所截,剩下部分母线长的最大值为a,最小值为b,那么圆柱被截后剩下部分的体积是 .