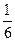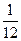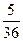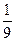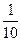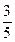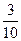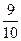题目内容
已知盒中有大小相同的3个红球和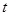
个白球，从盒中一次性取出3个球，取到白
球个数的期望为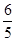
，若每次不放回的从盒中取一个球，一直到取出所有白球时停止抽取，
则停止抽取时恰好取到两个红球的概率为 （ ）
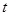个白球，从盒中一次性取出3个球，取到白球个数的期望为
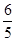，若每次不放回的从盒中取一个球，一直到取出所有白球时停止抽取，则停止抽取时恰好取到两个红球的概率为 （ ）
A． | B． | C． | D． |
D
取到白球个数的期望为
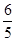，取得红球个数的期望为
（加起来是3），所以红球、白球比为3:2,所以白球有2个，一直到取出所有白球时停止抽取，恰好取到两个红球，则第四个抽取的一定是白球，可能的情况有：红红白白，红白红白，白红红白，则概率为：
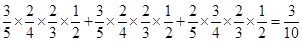
练习册系列答案
相关题目
.
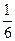）骰子，其中
表示第
枚骰子出现的点数，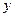
表示第
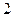枚骰子出现的点数。
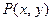在直线
上的概率；
的概率。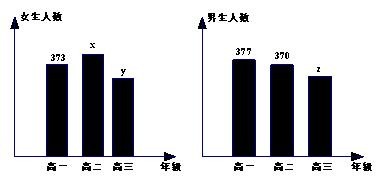
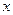的值；
全校抽取48名学生，问应在高三年级抽取多少名？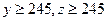
，求高三年级中女生比男生多的概率．
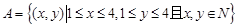内任取一个元素，则满足不等式
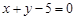的概率是________________ ．
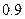，每粒种子能成长为幼苗的概率为
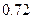，则在这批种子中，出芽后
的幼苗成活率为 。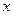
，第二次向上的点数记为
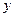，在直角坐标系
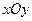中，以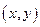
为坐标的点落在直线
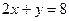上的概率为（ ）
