题目内容
有下列命题:①若四边形的四边相等,则这个四边形一定菱形;②在正方体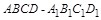
中,分别是棱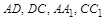 的中点,则直线
的中点,则直线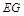 与
与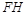 一定相交,且交点在直线
一定相交,且交点在直线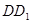 上;③若点
上;③若点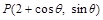 ,
,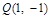 ,则
,则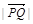 的最大值是
的最大值是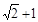 ;④若
;④若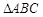 的顶点A、B分别是椭圆
的顶点A、B分别是椭圆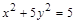 两个焦点,且满足
两个焦点,且满足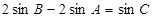 ,则顶点C的轨迹方程是双曲线.
,则顶点C的轨迹方程是双曲线.
其中所有正确命题的序号是 .
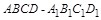
中,分别是棱
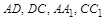 的中点,则直线
的中点,则直线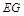 与
与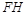 一定相交,且交点在直线
一定相交,且交点在直线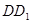 上;③若点
上;③若点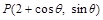 ,
,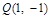 ,则
,则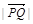 的最大值是
的最大值是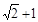 ;④若
;④若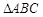 的顶点A、B分别是椭圆
的顶点A、B分别是椭圆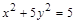 两个焦点,且满足
两个焦点,且满足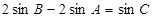 ,则顶点C的轨迹方程是双曲线.
,则顶点C的轨迹方程是双曲线.其中所有正确命题的序号是 .
②③
试题分析:①四边形有可能是空间四边形;②根据公理3可知正确;
③
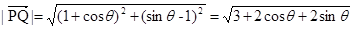
 ,所以最大值为
,所以最大值为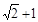 ;
;④因为
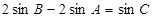 ,所以由正弦定理,容易得到:|CB|-|CA|=
,所以由正弦定理,容易得到:|CB|-|CA|=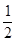 |AB|。
|AB|。因为A、B分别是椭圆
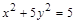 的左、右焦点,所以|AB|为定值,即
的左、右焦点,所以|AB|为定值,即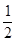 |AB|为定值,
|AB|为定值,所以点C的轨迹是以A、B为焦点,
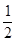 |AB|为实轴长的双曲线右半支。
|AB|为实轴长的双曲线右半支。点评:如①如果放在同一平面内,则为真命题,在空间中则为假命题,是本题的易忽略点。一般的,在平面上经常见到的说法正确到空间中不一定成立;在运用双曲线的定义时,应特别注意定义中的条件:差的绝对值。弄清是指整条双曲线还是双曲线的一支以及是哪一支。

练习册系列答案
相关题目
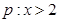 是
是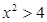 的充要条件;命题
的充要条件;命题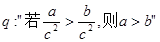 ,则( )
,则( )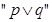 为真
为真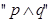 为真
为真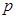 真
真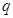 假
假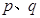 均为假
均为假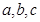
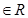 ,则“2b=a+c”是“a,b,c三个数成等差数列”的
,则“2b=a+c”是“a,b,c三个数成等差数列”的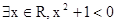 ”的否定是______________
”的否定是______________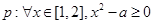 .命题
.命题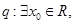 使得
使得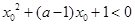 ;若“
;若“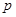 或
或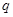 为真,
为真,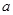 的取值范围.
的取值范围.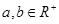 ,那么“
,那么“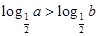 ”是 “
”是 “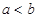 ”的( )
”的( )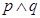 ”为假,且
”为假,且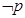 为假,则( )
为假,则( )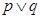 ”为假
”为假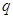 假
假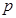 假
假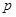 :关于
:关于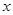 的不等式
的不等式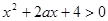 ,对一切
,对一切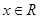 恒成立,命题
恒成立,命题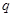 :函数
:函数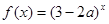 是增函数,若
是增函数,若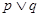 为真,
为真,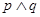 为假,求实数
为假,求实数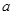 的取值范围.
的取值范围.