题目内容
编号为1,2,3,4,5的五个人,分别坐在编号为1,2,3,4,5的座位上,则至多有两个号码一致的坐法种数为( )A.120
B.119
C.110
D.109
【答案】分析:求出5个人的编号与座位的全部一致的方法数、只有4个人的编号与座位号一致的方法数、只有3个人的编号与作为号码一致的方法数.用所有的方法数减去以上3个值,即得所求.
解答:解:若5个人的编号与座位的全部一致,只有1种方法.
若只有4个人的编号与座位号一致,只有0种方法.
若只有3个人的编号与作为号码一致,只有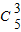 =10种方法.
=10种方法.
而所有的情况共有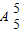 =120种,故至多有两个号码一致的坐法种数为 120-1-0-10=109,
=120种,故至多有两个号码一致的坐法种数为 120-1-0-10=109,
故选D.
点评:本题考查排列组合及简单计数问题,体现了分类讨论的数学思想,属于中档题.
解答:解:若5个人的编号与座位的全部一致,只有1种方法.
若只有4个人的编号与座位号一致,只有0种方法.
若只有3个人的编号与作为号码一致,只有
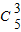 =10种方法.
=10种方法.而所有的情况共有
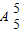 =120种,故至多有两个号码一致的坐法种数为 120-1-0-10=109,
=120种,故至多有两个号码一致的坐法种数为 120-1-0-10=109,故选D.
点评:本题考查排列组合及简单计数问题,体现了分类讨论的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
编号为1,2,3,4,5,6的六个同学排成一排,3、4号两位同学相邻,不同的排法( )
| A、60种 | B、120种 | C、240种 | D、480种 |
 (1)编号为A,B,C,D,E的五个小球放在如图所示的五个盒子里,要求每个盒子只能一个小球,且A球不能放在1,2号,B球必须放在与A球相邻的盒子中,不同的放法有多少种?
(1)编号为A,B,C,D,E的五个小球放在如图所示的五个盒子里,要求每个盒子只能一个小球,且A球不能放在1,2号,B球必须放在与A球相邻的盒子中,不同的放法有多少种?