题目内容
已知平面区域
内有一个圆,向该区域内随机投点,将点落在圆内的概率最大时的圆记为⊙M,此时的概率P为
.
|
| 9π |
| 32 |
| 9π |
| 32 |
分析:先画出该平面区域,明确区域所围成的平面图形的形状,再由“落在圆内的概率最大时的圆”则为该平面图形的内切圆.再由圆的相关条件求出圆的圆心以及半径,再与三角形的面积相比即可得到结论.
解答: 画出该区域得三角形ABC,顶点坐标分别为B(-1,0),C(3,0),A(1,4).
画出该区域得三角形ABC,顶点坐标分别为B(-1,0),C(3,0),A(1,4).
由于概率最大,故圆M是ABC内切圆,
因为BC的中垂线为X=1,AC的中垂线为y-2=
(x-2),
联立可得M(1,
),所以r=
.
∵S△ABC=
•BC•yA=
×4×4=8.
s圆=πr2=
π.
∴p=
=
.
故答案为:
.
 画出该区域得三角形ABC,顶点坐标分别为B(-1,0),C(3,0),A(1,4).
画出该区域得三角形ABC,顶点坐标分别为B(-1,0),C(3,0),A(1,4).由于概率最大,故圆M是ABC内切圆,
因为BC的中垂线为X=1,AC的中垂线为y-2=
| 1 |
| 2 |
联立可得M(1,
| 3 |
| 2 |
| 3 |
| 2 |
∵S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
s圆=πr2=
| 9 |
| 4 |
∴p=
| S圆 |
| S△ABC |
| 9π |
| 32 |
故答案为:
| 9π |
| 32 |
点评:本题主要考查平面区域的画法,内切圆的求法以及计算能力.解决本题的关键在于根据已知条件求出内切圆的圆心和半径.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
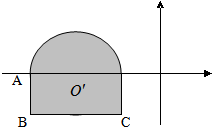 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1). 取得最小值,求m的值。
取得最小值,求m的值。 已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).
已知平面区域(含边界,上半部分为半圆,下半部分为矩形)如图,动点A(x,y)在该平面区域内,已知A(-3,0),C(-1,-1).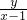 的取值范围;
的取值范围;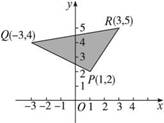 已知平面区域D由
已知平面区域D由 取得最小值,求m的值。
取得最小值,求m的值。