题目内容
1.用在矩阵行列式中所学的知识和方法,解方程组:$\left\{\begin{array}{l}mx+y=-1\\ 3mx-my=2m+3\end{array}\right.$.分析 先求出D=$|\begin{array}{l}{m}&{1}\\{3m}&{-m}\end{array}|$=-m2-3m,当D≠0时,原方程组有唯一的解;当D=0时,原方程组无解或有无数个解.
解答 解:∵$\left\{\begin{array}{l}mx+y=-1\\ 3mx-my=2m+3\end{array}\right.$,
∴D=$|\begin{array}{l}{m}&{1}\\{3m}&{-m}\end{array}|$=-m2-3m,
当D=-m2-3m≠0,即m≠0且m≠-3时,
方程组有唯一的解$x=\frac{1}{D}$$|\begin{array}{l}{-1}&{1}\\{2m+3}&{-m}\end{array}|$=$\frac{1}{m}$,y=$\frac{1}{D}$$|\begin{array}{l}{m}&{-1}\\{3m}&{2m+3}\end{array}|$=-2.
当D=-m2-3m=0,即m=0或m=-3时,原方程无解或有无数个解.
点评 本题考查二元一次方程组的矩阵形式的解法及应用,是基础题,解题时要注意系数矩阵的性质的合理运用.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
12.函数f(x)=4mx+2-3m在区间[-2,2]上存在t,使f(t)=0(t≠±2),则m的取值范围是( )
| A. | -$\frac{2}{5}$<m<$\frac{2}{11}$ | B. | m<-$\frac{2}{5}$ | C. | m>$\frac{2}{11}$ | D. | m<-$\frac{2}{5}$或m>$\frac{2}{11}$ |
9.△ABC中,角A,B,C所对的边分别为a,b,c,且cosAcosB=sinAsinB,则△ABC为( )
| A. | 直角三角形 | B. | 锐角三角形 | ||
| C. | 等腰直角三角形 | D. | 等腰或直角三角形 |
16.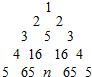 给出以下数阵,按各数排列规律,则n的值为( )
给出以下数阵,按各数排列规律,则n的值为( )
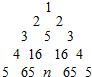 给出以下数阵,按各数排列规律,则n的值为( )
给出以下数阵,按各数排列规律,则n的值为( )| A. | 66 | B. | 256 | C. | 257 | D. | 326 |
6.已知△ABC,若对任意t∈R,|$\overrightarrow{BA}-t\overrightarrow{BC}$|≥|$\overrightarrow{AC}$|恒成立,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |