题目内容
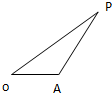 如图,已知△OAP的面积为S,
如图,已知△OAP的面积为S,| OA |
| AP |
| 1 |
| 2 |
| OA |
| AP |
分析:由题意可得 OA•OP cos∠AOP=1,且
<
•OA•OP•sin∠AOP<2,可得 1<tan∠AOP<4,从而
<∠AOP<arctan4.
| 1 |
| 2 |
| 1 |
| 2 |
| π |
| 4 |
解答:解:由题意可得 OA•OP cos∠AOP=1,且
<
•OA•OP•sin∠AOP<2,
∴1<
<4,∴1<tan∠AOP<4,∴
<∠AOP<arctan4,
故答案为:(
,arctan4).
| 1 |
| 2 |
| 1 |
| 2 |
∴1<
| sin∠AOP |
| cos∠AOP |
| π |
| 4 |
故答案为:(
| π |
| 4 |
点评:本题考查两个向量的数量积的定义,根据三角函数的值的范围,求出角的范围,得到 1<tan∠AOB<4,
是解题的关键,属于中档题.
是解题的关键,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
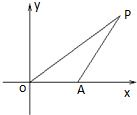 如图,已知△OAP的面积为S,
如图,已知△OAP的面积为S,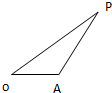 如图,已知△OAP的面积为S,
如图,已知△OAP的面积为S,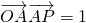 .如果
.如果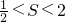 ,那么向量
,那么向量 与
与 的夹角θ的取值范围是________.
的夹角θ的取值范围是________.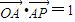 .设
.设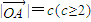 ,
,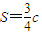 ,并且以O为中心、A为焦点的椭圆经过点P.当
,并且以O为中心、A为焦点的椭圆经过点P.当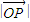 取得最小值时,则此椭圆的方程为 .
取得最小值时,则此椭圆的方程为 .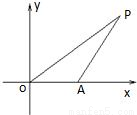
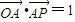 .如果
.如果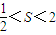 ,那么向量
,那么向量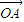 与
与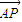 的夹角θ的取值范围是 .
的夹角θ的取值范围是 .