题目内容
(本小题满分12分)
设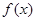
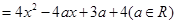 ,若方程
,若方程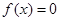 有两个均小于2的不同的实数根,则此时关于
有两个均小于2的不同的实数根,则此时关于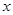 的不等式
的不等式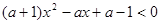 是否对一切实数
是否对一切实数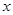 都成立?并说明理由。
都成立?并说明理由。
设
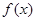
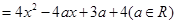 ,若方程
,若方程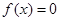 有两个均小于2的不同的实数根,则此时关于
有两个均小于2的不同的实数根,则此时关于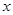 的不等式
的不等式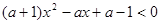 是否对一切实数
是否对一切实数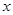 都成立?并说明理由。
都成立?并说明理由。只有在 时,
时,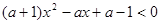 才对任意实数
才对任意实数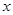 都成立。
都成立。
 时,
时,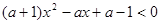 才对任意实数
才对任意实数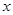 都成立。
都成立。试题分析:由题意得

得
 ;
;若
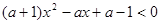 对任意实数
对任意实数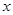 都成立,则有:
都成立,则有:(1)若
 =0,即
=0,即 ,则不等式化为
,则不等式化为 不合题意
不合题意(2)若

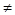 0,则有
0,则有
得
 ,
,综上可知,只有在
 时,
时,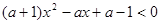 才对任意实数
才对任意实数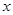 都成立。
都成立。∴这时
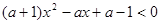 不对任意实数
不对任意实数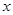 都成立
都成立点评:对于二次函数f(x)=ax2+bx+c=0(a≠0)在实数集R上恒成立问题可利用判别式直接求解,即 :f(x)>0恒成立


 ;f(x)<0恒成立
;f(x)<0恒成立

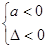 ,若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.
,若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.
练习册系列答案
相关题目
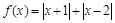 ,不等式
,不等式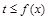 在
在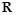 上恒成立.
上恒成立.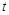 的取值范围;
的取值范围;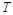 ,若正实数
,若正实数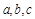 满足
满足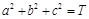 ,求
,求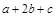 的最大值.
的最大值.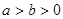 ,则下列不等式不成立的是( )
,则下列不等式不成立的是( ) 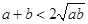



 的解集是( )
的解集是( )



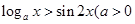 且
且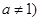 对任意
对任意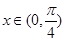 都成立,则
都成立,则 的取值
的取值



 是使表达式
是使表达式 成立的最小整数,则方程
成立的最小整数,则方程 实根的个数为___ ___.
实根的个数为___ ___. ,则( )
,则( )



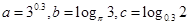 则
则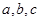 的大小关系是
的大小关系是 



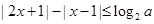 (其中
(其中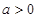 )。
)。