题目内容
△ABC的内角A、B、C的对边分别为a、b、c.
(1)若A、B、C成等差数列,求B的值;
(2)若a、b、c成等比数列,求sinB+
cosB的取值范围.
(1)若A、B、C成等差数列,求B的值;
(2)若a、b、c成等比数列,求sinB+
| 3 |
(1)△ABC中,∵A、B、C成等差数列,
∴2B=A+C;
又A+B+C=π,
∴B=
,
即B的值是
;
(2)△ABC中,∵a、b、c成等比数列,
∴b2=ac,
又∵a2+c2≥2ac,
∴cosB=
≥
=
,
当且仅当a=c时取等号,
∴0<B≤
,
又sinB+
cosB=2(
sinB+
cosB)=2sin(B+
),
∴B+
∈(
,
],
∴
≤2sin(B+
)≤2,
∴sinB+
cosB的取值范围[
,2].
∴2B=A+C;
又A+B+C=π,
∴B=
| π |
| 3 |
即B的值是
| π |
| 3 |
(2)△ABC中,∵a、b、c成等比数列,
∴b2=ac,
又∵a2+c2≥2ac,
∴cosB=
| a2+c2-b2 |
| 2ac |
| 2ac-ac |
| ac |
| 1 |
| 2 |
当且仅当a=c时取等号,
∴0<B≤
| π |
| 3 |
又sinB+
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 3 |
∴B+
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
∴
| 3 |
| π |
| 3 |
∴sinB+
| 3 |
| 3 |

练习册系列答案
相关题目
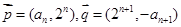 ,n∈N*,向量
,n∈N*,向量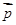 与
与 垂直,且a1=1.
垂直,且a1=1.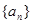 中,
中, 则数列
则数列