题目内容
(2013•重庆)从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得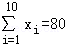 ,
, ,
, ,
,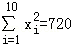 .
.
(1)求家庭的月储蓄y对月收入x的线性回归方程y=bx+a;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
附:线性回归方程y=bx+a中, ,
,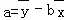 ,其中
,其中 ,
, 为样本平均值,线性回归方程也可写为
为样本平均值,线性回归方程也可写为 .
.
(1)y=0.3x﹣0.4;
(2)由(1)可知b=0.3>0,即变量y随x的增加而增加,故x与y之间是正相关;
(3)把x=7代入回归方程可预测该家庭的月储蓄为y=0.3×7﹣0.4=1.7(千元)
解析

练习册系列答案
相关题目
为调查某市老年人是否需要志愿者提供帮助,用简单随机抽样方法从该市调查了500位老年人,结果如右表.
| 性别 是否需要志愿者 | 男 | 女 |
| 需要 | 40 | 30 |
| 不需要 | 160 | 270 |
(1)估计该市老年人中, 需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该市的老年人是否需要志愿者提供帮助与性别有关?
附:
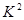
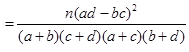 (
(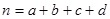 )
)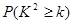 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
| | 支持A方案 | 支持B方案 | 支持C方案 |
| 35岁以下 | 200 | 400 | 800 |
| 35岁以上(含35岁) | 100 | 100 | 400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
某学校高一年学生在某次数学单元测试中,成绩在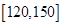 的频数分布表如下:
的频数分布表如下:
| 分数 |  | 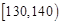 | 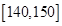 |
| 频数 | 60 | 20 | 20 |
(1)用分层抽样的方法从成绩在
 ,
,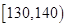 和
和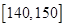 的同学中共抽取
的同学中共抽取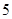 人,其中成绩在
人,其中成绩在 的有几人?
的有几人?(2)从(1)中抽出的
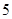 人中,任取
人中,任取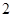 人,求成绩在
人,求成绩在 和
和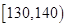 中各有
中各有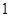 人的概率?
人的概率? 随着工业化以及城市车辆的增加,城市的空气污染越来越严重,空气质量指数API一直居高不下,对人体的呼吸系统造成了严重的影响.现调查了某市500名居民的工作场所和呼吸系统健康,得到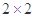 列联表如下:
列联表如下:
| | 室外工作 | 室内工作 | 合计 |
| 有呼吸系统疾病 | 150 | | |
| 无呼吸系统疾病 | | 100 | |
| 合计 | 200 | | |
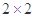 列联表;
列联表;(2)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(3)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机的抽取两人,求两人都有呼吸系统疾病的概率.
参考公式与临界值表:K2=
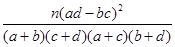
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
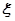 的分布列。
的分布列。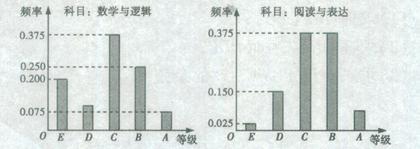
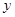 (万元)和房屋的面积
(万元)和房屋的面积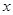 (
( )的数据 ,若由资料可知
)的数据 ,若由资料可知
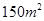 时的销售价格.
时的销售价格.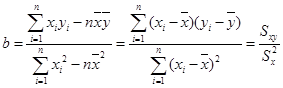

 ,
, ,
,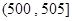 ,
, ,
,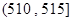 ,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题:
,得到样本的频率分布直方图(如图所示).若规定重量超过495克但不超过510克的产品为合格产品,且视频率为概率,回答下列问题: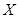 为合格产品的数量,求
为合格产品的数量,求 ;
;