题目内容
已知双曲线C的两条渐近线都过原点,且都与以点A(| 2 |
| 2 |
分析:先根据双曲线的顶点坐标确定焦点在y轴上,进而可确定a的值,然后设出双曲线的方程,根据其渐近线与以点A(
,0)为圆心,1为半径的圆相切可得到点A(
,0)到渐近线的距离等于1,进而可求出b的值,确定答案.
| 2 |
| 2 |
解答:解:∵双曲线的一个顶点是(0,
),
∴双曲线的焦点在y轴上,且a=
故,双曲线方程可设为:
-
=1,且渐近线为
x±by=0
又∵
=1∴b2=2
故双曲线方程为:y2-x2=2
| 2 |
∴双曲线的焦点在y轴上,且a=
| 2 |
故,双曲线方程可设为:
| y2 |
| 2 |
| x2 |
| b2 |
| 2 |
又∵
|
| ||||
|
故双曲线方程为:y2-x2=2
点评:本题主要考查双曲线的简单性质.考查对基础知识的掌握程度,属于基础题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
 ,0)为右焦点的双曲线C的离心率,
,0)为右焦点的双曲线C的离心率,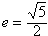 。
。