Question

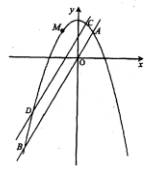
（08年安庆市二模理）（12分）        设点A、B是直线与抛物线的两个交点，抛物线上的动点M在A、B两点间移动，如图所示。

         （1）试求M的坐标，使得△MAB的面积最大；

         （2）试证明：抛物线上平行于AB的弦恒被一条定直线平分。

 

Answer 1

解析：（1）设点M的坐标为,由于线段AB的长是定值,所以只要点M到直线AB的距离最大即可.平行移动AB到与抛物线相切的位置时,切点到直线AB的距离最大.因为,,于是代入中得,因此当点M的坐标为时, 使得△MAB的面积最大.          …………… 6分

（2）设抛物线平行于直线AB的弦的方程为弦的两个端点为、，则所以

即.若设弦的中点为,则x=－1,即弦的中点的轨迹方程为x=－1,因此抛物线上平行于AB的弦恒被一条直线平分   .....12分