题目内容
4. 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,M为AB的中点,△PAD为等边三角形,且平面PAD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,∠DAB=60°,AB=2AD,M为AB的中点,△PAD为等边三角形,且平面PAD⊥平面ABCD.(Ⅰ)证明:PM⊥BC.
(Ⅱ)若PD=1,求点D到平面PAB的距离.
分析 (Ⅰ)取AD中点O,连接PO,OM,DM,证明BC⊥平面POM,可得PM⊥BC.
(Ⅱ)若PD=1,利用VP-ABD=VD-PAB,可求点D到平面PAB的距离.
解答 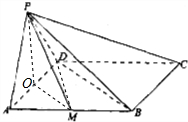 (Ⅰ)证明:取AD中点O,连接PO,OM,DM,
(Ⅰ)证明:取AD中点O,连接PO,OM,DM,
由已知得PO⊥平面ABCD,
∴PO⊥BC,
∵∠DAB=60°,AB=2AD,
∴△ADM是正三角形,
∴OM⊥AD,OM∥BD,OM=$\frac{1}{2}$BD,
∴OM⊥BC
∵PO∩OM=O,
∴BC⊥平面POM,
∵PM?平面POM,
∴PM⊥BC.
(Ⅱ)解:∵PD=1,∠DAB=60°,AB=2AD=2PD=2,
∴△ABD是直角三角形,BD⊥AD,
∴BD=$\sqrt{3}$,
∵PO=$\frac{\sqrt{3}}{2}$,
∴VP-ABO=$\frac{1}{3}{S}_{△ABD}•PO$=$\frac{1}{4}$
设点D到平面P取AB的距离为h,
由BD⊥AD,BD⊥PO,
∴BD⊥平面ABD,
∴BD⊥PD,
∴△PBD是直角三角形,
∴PB=2,
在△PBD中,PA=1,AB=PB=2,
∴△PBD是等腰三角形,
∴S△PAB=$\frac{\sqrt{15}}{4}$,
∴由VP-ABD=VD-PAB,可得$\frac{1}{3}•\frac{\sqrt{15}}{4}h$=$\frac{1}{4}$,
∴h=$\frac{\sqrt{15}}{5}$,
∴点D到平面PAB的距离为$\frac{\sqrt{15}}{5}$.
点评 本题考查线面垂直,考查点D到平面PAB的距离的计算,正确运用线面垂直的判定,利用等体积是关键.

练习册系列答案
相关题目
12.将函数$f(x)=cos({x+\frac{π}{3}})$的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,所得图象的一条对称轴方程可能是( )
| A. | $x=\frac{π}{3}$ | B. | $x=-\frac{π}{6}$ | C. | $x=-\frac{π}{3}$ | D. | $x=-\frac{2π}{3}$ |
19.随着人口老龄化的到来,我国的劳动力人口在不断减少,“延迟退休”已经成为人们越来越关注的话题,为了了解公众对“延迟退休”的态度,某校课外研究性学习小组对某社区随机抽取了5人进行调查,将调查情况进行整理后制成下表:
年龄在[25,30),[55,60)的被调查者中赞成人数分别是3人和2人,现从这两组的被调查者中各随机选取2人,进行跟踪调查.
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都是赞成的概率;
(Ⅱ)求选中的4人中,至少有3人赞成的概率;
(Ⅲ)若选中的4人中,不赞成的人数为X,求随机变量X的分布列和数学期望.
| 年龄 | [20,25) | [25,30) | [30,35) | [35,40) | [40,45) |
| 人数 | 4 | 5 | 8 | 5 | 3 |
| 年龄 | [45,50) | [50,55) | [55,60) | [60,65) | [65,70) |
| 人数 | 6 | 7 | 3 | 5 | 4 |
(Ⅰ)求年龄在[25,30)的被调查者中选取的2人都是赞成的概率;
(Ⅱ)求选中的4人中,至少有3人赞成的概率;
(Ⅲ)若选中的4人中,不赞成的人数为X,求随机变量X的分布列和数学期望.
13.为得到函数f(x)=cosx-$\sqrt{3}$sinx,只需将函数y=$\sqrt{2}cosx+\sqrt{2}$sinx( )
| A. | 向左平移$\frac{5π}{12}$ | B. | 向右平移$\frac{5π}{12}$ | C. | 向左平移$\frac{7π}{12}$ | D. | 向右平移$\frac{7π}{12}$ |
 “无字证明”(proofs without words)就是将数学命题用简单、有创意而且易于理解的几何图形来呈现,请利用下面两个三角形(△ACD和△ECD)的面积关系,写出高中数学中的一个重要关系式:$\sqrt{ab}≤\frac{1}{2}(a+b)$.
“无字证明”(proofs without words)就是将数学命题用简单、有创意而且易于理解的几何图形来呈现,请利用下面两个三角形(△ACD和△ECD)的面积关系,写出高中数学中的一个重要关系式:$\sqrt{ab}≤\frac{1}{2}(a+b)$. 如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=AD,PD⊥底面ABCD,
如图,四棱锥P-ABCD中,底面ABCD是平行四边形,且AB=AD,PD⊥底面ABCD,