题目内容
【题目】已知数列![]() 和
和![]() 满足:
满足:![]() ,
,![]() 其中
其中![]() 为实数,
为实数,![]() 为正整数.
为正整数.
(1)对任意实数![]() ,证明数列
,证明数列![]() 不是等比数列;
不是等比数列;
(2)对于给定的实数![]() ,试求数列
,试求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在实数
,是否存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() 成立?若存在,求
成立?若存在,求![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(1)证明见解析;(2) 当![]() ,
, ![]() ;当
;当![]() 时,
时, ;
;
(3) 当![]() 时,得
时,得![]() ,不存在实数满足要求;
,不存在实数满足要求;
当![]() 时,存在实数
时,存在实数![]() ,其取值范围是
,其取值范围是![]()
【解析】
(1)代入![]() 求
求![]() 证明矛盾即可.
证明矛盾即可.
(2) 由![]() ,代入
,代入![]() 可得
可得![]() 再分情况
再分情况![]() 与
与![]() 的情况进行讨论即可.
的情况进行讨论即可.
(3)由第(2)问求得的 ,代入
,代入![]() 再参变分离求解即可.
再参变分离求解即可.
(1)假设存在一个实数![]() ,使
,使![]() 是等比数列,,
是等比数列,,
由![]() ,分别令
,分别令![]() 有
有![]() ,
,
![]() .又
.又![]()
即![]() ,矛盾,
,矛盾,
所以![]() 不是等比数列.
不是等比数列.
(2)因为![]()
![]() ,又
,又![]() ,
,
所以当![]() ,
,![]() ,此时
,此时![]() .
.
当![]() 时,
时,![]() ,
,![]() ,
,
此时,数列![]() 是以
是以![]() 为首项,
为首项,![]() 为公比的等比数列.
为公比的等比数列.
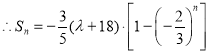
(3)要使![]() 对任意正整数
对任意正整数![]() 成立,
成立,
则![]() ,∴
,∴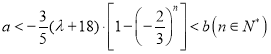
得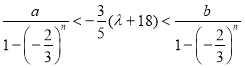 .
.
令![]() ,则当
,则当![]() 为正奇数时,
为正奇数时,![]() ;当
;当![]() 为正偶数时,
为正偶数时,![]() ,
,
![]() 的最大值为
的最大值为![]() ,
,![]() 的最小值为
的最小值为![]() .
.
故![]() ,即
,即![]()
当![]() 时,得
时,得![]() ,不存在实数满足要求;
,不存在实数满足要求;
当![]() 时,存在实数
时,存在实数![]() ,使得对任意正整数
,使得对任意正整数![]() ,都有
,都有![]() 成立,且
成立,且![]() 的取值范围是
的取值范围是![]()

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
分数段 |
|
|
|
|
| 1∶1 | 2∶1 | 3∶4 | 4∶5 |

(1)求图中![]() 的值;
的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(![]() )与数学成绩相应分数段的人数(
)与数学成绩相应分数段的人数(![]() )之比如下表所示,求数学成绩在
)之比如下表所示,求数学成绩在![]() 之外的人数.
之外的人数.