题目内容
 设全集为U=R,集合A={x|(x+3)(6-x)≤0},B={x|log2(x+2)<4}.
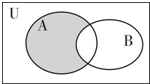
设全集为U=R,集合A={x|(x+3)(6-x)≤0},B={x|log2(x+2)<4}.(1)求如图阴影部分表示的集合;
(2)已知C={x|x>2a且x<a+1},若C⊆B,求实数a的取值范围.
分析:(1)根据维恩图确定阴影部分表示的集合;
(2)利用条件C⊆B,建立不等式关系,即可求实数a的取值范围.
(2)利用条件C⊆B,建立不等式关系,即可求实数a的取值范围.
解答:解:(1)由(x+3)(x-6)≥0,得x≥6或x≤-3,即A=(-∞,-3]∪[6,+∞),
由0<x+2<16,解得-2<x<14,即B=(-2,14),
∵阴影部分为A∩CRB,
∴A∩CRB=(-∞,-3]∪[14,+∞).
(2)∵C={x|x>2a且x<a+1},
∴①2a≥a+1,即a≥1时,C=∅,成立;
②2a<a+1,即a<1时,C=(2a,a+1)⊆(-2,14),
则
,
解得-1≤a<1.
综上所述,a的取值范围为[-1,+∞).
由0<x+2<16,解得-2<x<14,即B=(-2,14),
∵阴影部分为A∩CRB,
∴A∩CRB=(-∞,-3]∪[14,+∞).
(2)∵C={x|x>2a且x<a+1},
∴①2a≥a+1,即a≥1时,C=∅,成立;
②2a<a+1,即a<1时,C=(2a,a+1)⊆(-2,14),
则
|
解得-1≤a<1.
综上所述,a的取值范围为[-1,+∞).
点评:本题主要考查维恩的识别和判断,集合的基本运算以及集合关系的应用,注意对集合C要注意讨论.

练习册系列答案
 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案
相关题目
 设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|log2(x+2)<4}.
设全集为U=R,集合A=(-∞,-3]∪[6,+∞),B={x|log2(x+2)<4}.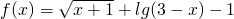 的定义域,B={x|2x-4≥x-2}
的定义域,B={x|2x-4≥x-2}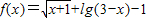 的定义域,B={x|2x-4≥x-2}
的定义域,B={x|2x-4≥x-2}