题目内容
给出下列五个判断:①若非零向量
 、
、 满足
满足 ,则向量
,则向量 、
、 所在的直线互相平行或重合;
所在的直线互相平行或重合;②在△ABC中,
 ;
;③已知向量
 、
、 为非零向量,若
为非零向量,若 ,则
,则 ;
;④向量
 、
、 满足
满足 ,则
,则 ;
;⑤已知向量
 、
、 为非零向量,则有
为非零向量,则有 .
.其中正确的是 .(填入所有正确的序号)
【答案】分析:①②由向量共线的定义与运算性质得①②正确.
③向量进行数量积运算时不能进行约分.
④ 所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.
所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.
⑤向量的运算律不满足结合律.
解答:解:①由向量共线的定义得①正确.
②利用向量的运算性质得 所以②正确.
所以②正确.
③向量进行数量积运算时不能进行约分.
④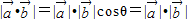 所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.
所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.
⑤向量的运算律不满足结合律.
点评:本题主要考查数列有关的定义与运算律以及运算性质,解决此类题目的关键是准确记忆相关结论,细心运算.
③向量进行数量积运算时不能进行约分.
④
 所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.
所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.⑤向量的运算律不满足结合律.
解答:解:①由向量共线的定义得①正确.
②利用向量的运算性质得
 所以②正确.
所以②正确.③向量进行数量积运算时不能进行约分.
④
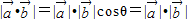 所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.
所以cosθ=0,所以两个向量的夹角是0°或180°,所以④正确.⑤向量的运算律不满足结合律.
点评:本题主要考查数列有关的定义与运算律以及运算性质,解决此类题目的关键是准确记忆相关结论,细心运算.

练习册系列答案
相关题目