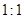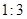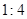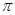题目内容
三棱锥 的四个顶点都在球面上,SA是球的直径,
的四个顶点都在球面上,SA是球的直径, ,
, ,则该球的表面积为( )
,则该球的表面积为( )
A. | B. | C. | D. |

B
解析试题分析:N为等边三角形SBC的外心,连结SN,并延长交BC于M,则M是BC中点,∴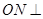 平面
平面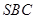 ,
,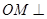 平面ABC,
平面ABC,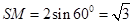 ,则
,则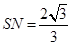 ,
,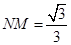 ,
,
在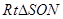 中,
中,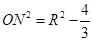 ,在
,在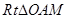 中,
中,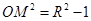 ,
,
∴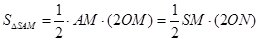 ,∴
,∴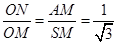 ,
,
∴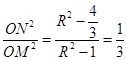 ,即
,即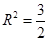 ,
,
∴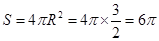 .
.
考点:球的表面积、勾股定理、三角形面积公式.

练习册系列答案
相关题目
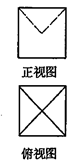
在空间中有一棱长为 的正四面体,其俯视图的面积的最大值为( )
的正四面体,其俯视图的面积的最大值为( )
A. | B. | C. | D. |
已知四面体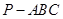 的外接球的球心
的外接球的球心 在
在 上,且
上,且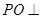 平面
平面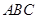 ,
,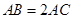 ,若四
,若四
面体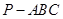 的体积为
的体积为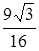 ,则该球的表面积为( )
,则该球的表面积为( )
A.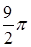 | B.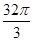 | C. | D.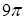 |
用与球心距离为1的平面去截球,所得的截面面积为π,则球的体积为( )
A.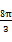 | B.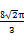 | C.8 π π | D. |
 圆柱
圆柱  圆锥
圆锥  四面体
四面体  三棱柱
三棱柱 ;直径为2的球的体积为
;直径为2的球的体积为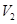 。则
。则 ( )
( )