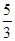题目内容
在空间中有一棱长为 的正四面体,其俯视图的面积的最大值为( )
的正四面体,其俯视图的面积的最大值为( )
A. | B. | C. | D. |
B
解析试题分析:如图所示的正方体 ,设其面对角线长为
,设其面对角线长为 ,则四面体
,则四面体 为正四面体,
为正四面体,
且其棱长为 ,四面体
,四面体 在平面
在平面 内的投影图形为正方形
内的投影图形为正方形 ,易求得正方体的棱长为
,易求得正方体的棱长为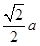 ,因此正方形
,因此正方形 的面积为
的面积为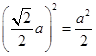 ,且
,且 ,将正方体
,将正方体 ,设
,设 、
、 、
、 、
、 在俯视图中的投影点分别为
在俯视图中的投影点分别为 、
、 、
、 、
、 ,点
,点 、
、 在俯视图中的投影点分别为
在俯视图中的投影点分别为 、
、 ,则
,则 ,且四边形
,且四边形 与四边形
与四边形 的面积相等,且正四面体
的面积相等,且正四面体 的俯视图图形为四边形
的俯视图图形为四边形 ,设平面
,设平面 与俯视图平面所成的角为
与俯视图平面所成的角为 ,则
,则 ,
,
则 ,故当
,故当 时,四面体
时,四面体 的俯视图的面积取最大值
的俯视图的面积取最大值 ,
,
故选B.
考点:三视图

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
(2011•浙江)若某几何体的三视图如图所示,则这个几何体的直观图可以是( )
A. | B. | C. | D. |
如图,某几何体的三视图都是等腰直角三角形,则几何体的体积是( )
| A.8 | B.7 | C.9 | D.6 |
已知某个几何体的三视图如下,那么可得这个几何体的体积是( )
A. | B. | C.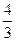 | D. |
正方体ABCD﹣A1B1C1D1中,E为线段B1D1上的一个动点,则下列结论中错误的是( )
| A.AC⊥BE |
| B.B1E∥平面ABCD |
| C.三棱锥E﹣ABC的体积为定值 |
| D.直线B1E⊥直线BC1 |


 C.4 D.
C.4 D.
 的四个顶点都在球面上,SA是球的直径,
的四个顶点都在球面上,SA是球的直径, ,
, ,则该球的表面积为( )
,则该球的表面积为( )