题目内容
给出下面结论：
①命题p：“?x0∈R，x
-3x0+2≥0”的否定为￢p：“?x∈R，x2-3x+2＜0”
②函数f（x）=2x+3x的零点所在区间是（-1，0）；
③函数y=sin2x的图象向左平移
个单位后，得到函数y=sin(2x+
)图象；
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α．
其中正确结论的个数是（ ）
①命题p：“?x0∈R，x
| 20 |
②函数f（x）=2x+3x的零点所在区间是（-1，0）；
③函数y=sin2x的图象向左平移
| π |
| 3 |
| π |
| 3 |
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α．
其中正确结论的个数是（ ）
| A．1 | B．2 | C．3 | D．4 |
①由特称命题的否定可知：命题p：“?x0∈R，x
-3x0+2≥0”的否定为￢p：“?x∈R，x2-3x+2＜0”，故正确；
②f（-1）=2-1-3=-
，f（-0）=20+3×0=1，满足f（-1）f（0）＜0，故函数f（x）=2x+3x在区间（-1，0）上有零点，
又函数f（x）单调递增，故有唯一的零点在区间（-1，0），故正确；
③函数y=sin2x的图象向左平移
个单位后，得到函数y=sin2（x+
）=sin（2x+
）的图象，而非y=sin(2x+
)图象，故错误；
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α，或n?α，故错误．
故选B
| 20 |
②f（-1）=2-1-3=-
| 5 |
| 2 |
又函数f（x）单调递增，故有唯一的零点在区间（-1，0），故正确；
③函数y=sin2x的图象向左平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α，或n?α，故错误．
故选B
练习册系列答案
相关题目
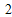-3x+2≥0”的否定为￢p：“?x∈R，x2-3x+2＜0”
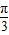个单位后，得到函数
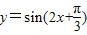图象；