题目内容
给出下面结论：
①命题p：“?x0∈R，x
-3x0+2≥0”的否定为￢p：“?x∈R，x2-3x+2＜0”
②函数f（x）=2x+3x的零点所在区间是（-1，0）；
③函数y=sin2x的图象向左平移
个单位后，得到函数y=sin(2x+
)图象；
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α．
其中正确结论的个数是（ ）
①命题p：“?x0∈R，x
2 0 |
②函数f（x）=2x+3x的零点所在区间是（-1，0）；
③函数y=sin2x的图象向左平移
| π |
| 3 |
| π |
| 3 |
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α．
其中正确结论的个数是（ ）
分析：①由特称命题的否定规律可作出判断；②代值可得f（-1）f（0）＜0，由零点的存在性定理可得结论；③由图象的平移规律，可得到函数y=sin2（x+
）=sin（2x+
）的图象，而非y=sin(2x+
)图象；④由条件可得n∥α，或n?α，不一定是n∥α．
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
解答：解：①由特称命题的否定可知：命题p：“?x0∈R，x
-3x0+2≥0”的否定为￢p：“?x∈R，x2-3x+2＜0”，故正确；
②f（-1）=2-1-3=-
，f（-0）=20+3×0=1，满足f（-1）f（0）＜0，故函数f（x）=2x+3x在区间（-1，0）上有零点，
又函数f（x）单调递增，故有唯一的零点在区间（-1，0），故正确；
③函数y=sin2x的图象向左平移
个单位后，得到函数y=sin2（x+
）=sin（2x+
）的图象，而非y=sin(2x+
)图象，故错误；
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α，或n?α，故错误．
故选B
2 0 |
②f（-1）=2-1-3=-
| 5 |
| 2 |
又函数f（x）单调递增，故有唯一的零点在区间（-1，0），故正确；
③函数y=sin2x的图象向左平移
| π |
| 3 |
| π |
| 3 |
| 2π |
| 3 |
| π |
| 3 |
④对于直线m，n和平面α，若m⊥α，m⊥n，则n∥α，或n?α，故错误．
故选B
点评：本题考查命题真假的判断，涉及命题的否定和零点以及函数图象的变换和空间中的线面位置关系，属基础题．
练习册系列答案
相关题目
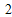-3x+2≥0”的否定为￢p：“?x∈R，x2-3x+2＜0”
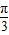个单位后，得到函数
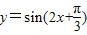图象；