题目内容
等比数列{an}的首项为a1=100，公比q=
，设f（n）表示这个数列的前n项的积，则当n=________时，f（n）有最大值．
7
分析：写出f（n）=a1a2a3…an，与f（n+1）作商，研究单调性即可．判断何时取最大值
解答：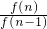
=
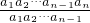=an=100×
=
，
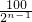当an≥1时，即2n-1≤100，n≤7时，f（n）单增，当an≤7时，即2n-1≥100，n≥8时，f（n）单减，
即当n=7时，f（n）有最大值．
故答案为7
点评：本题考查了等比数列通项公式、数列的单调性．是好题．
分析：写出f（n）=a1a2a3…an，与f（n+1）作商，研究单调性即可．判断何时取最大值
解答：
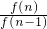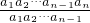==an=100×=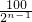，当an≥1时，即2n-1≤100，n≤7时，f（n）单增，当an≤7时，即2n-1≥100，n≥8时，f（n）单减，
即当n=7时，f（n）有最大值．
故答案为7
点评：本题考查了等比数列通项公式、数列的单调性．是好题．
练习册系列答案
世纪百通主体课堂小学课时同步达标系列答案
世纪百通优练测系列答案
百分学生作业本题练王系列答案
相关题目