题目内容
矩形ABCD中，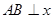
轴，且矩形ABCD恰好能完全覆盖函数
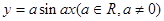的一个完整周期图象，则当
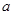变化时，矩形ABCD周长的最小值为 .
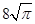
解析试题分析：由题意得到矩形ABCD长为 函数y=asinax（a∈R，a≠0）的最小正周期|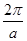 
|，宽为|2a|，利用基本不等式,求出周长的最小值．解：由题意得，矩形ABCD长为 函数y=asinax（a∈R，a≠0）的一个完整周期|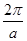|，宽为|2a|，故此矩形的周长为 2•|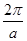|+2•|2a|=
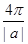+4|a|≥=8
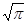，故答案为：8．
考点：基本不等式
点评：本题考查函数y=asinax（a∈R，a≠0）的最小正周期，基本不等式的应用，求出举行的长是解题的关键．
练习册系列答案
相关题目
满足
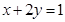，则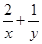
的最小值为 .
不在直线
的下方，则
的最小值为________．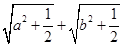
的取值范围是 . 
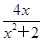的最大值为________________________．
，当
时，
取得最小值
，则
_______.
满足
，则
的最小值为_____________.
的最小值为 .